比較言語学における統計的研究法の可能性について

　言語の不思議は早くから自分の頭の中にかなり根深い疑問の種を植え付けていたもののようである。六七歳のころ、始めて従兄（いとこ）から英語の手ほどきを教えられた時に、最初に出会ったセンテンスは、たしか「猿（さる）が手を持つ」というのであった。その時、まず冠詞というものの「存在理由」がはなはだしく不可解なものに思われた。The（当時かなで書くとおりにジーと発音していた）が、至るところ文章の始めごとに繰り返されて出現する事が奇妙に強い印象を与えた事を記憶する。自分の手のことを「持つ」というのもおかしかったが、これが「手を」の前に来る事がはなはだしく不思議であった。
　今になって考えてみると、このジー、ジーという音の繰り返しは、当時の幼い頭の中に、まだ夢にも知らなかった、遠い遠い所にある、一つの別な珍しい世界からのかすかなおとずれのように響いたのかもしれない。それはとにかく、当時に感じた漠然（ばくぜん）たる不思議の感じは、年を経て外国語に対する知識の増すとともに、次第に増しはしても、決して減りはしなかった。ただそれが次第に具体的な疑問の形をとって意識されて来たのである。しかし四十余年前に漠然と感ぜられた疑問は今日に至っても依然たる不可解の疑問である。そして少しばかり言語に関する学者の所説などを読んでみても、なかなか簡単にこの疑問の答解は得られそうもないように思われた。
　英語やドイツ語とだんだんに教わるうちに、しばしば日本語とよく似た音をもった同義の語に出会う事がある。これは偶然であろうとは思っても、そのことごとくが偶然の暗合であるという事を証明する事もかなりにむつかしそうに思われた。
　自分のまだ学生時代に、ある学者が、日本の神話の舞台をギリシア近辺へ持って行こうとする大胆な説を公にして問題になった事がある。自分は直接にその所説の全部を読んだわけではなかったが、その説の一部をどこかで瞥見（べっけん）して、いろいろその所説に対する疑いを起こした事もあった。しかし単に説の奇矯（ききょう）であり、常識的に考えてありそうもないというだけの理由から、この説を初めから問題ともしないでいたずらに嘲笑（ちょうしょう）の的にしようとする人のみ多い事にも疑いをいだかないわけには行かなかった。少なくも東欧の一部と極東日本との間に万一存在したかもしれないなんらかの古い関係の可能性という事までも、なんの考察もなしに否定せんとする人のあまりに多いのに驚いた。もちろん当時これに関する言語学者間の意見がいかなるものであったか自分は知らない。ここで自分のいうのは、言語学者でない一般有識階級と称するものについてである。とにかくギリシア古代と日本古代との間になんらの交渉もなかったという事を科学的に証明する事をはたしてだれがあえてしうるであろうと疑ったこともある。
　十年ほど前に少しばかりロシア語の初歩を学んだ事もあった。それがために「言語の不思議」に対する自分の好奇心と疑問とは、むしろ急に大きな高い階段を一つ駆け上がったような気がした。そして、一方で新しい不思議が多量に加わると同時に、他方ではこの新しい不思議が、かえって古い不思議のなぞを解くかぎとなりうる可能性を暗示するようにも見えた。それは単に語彙（ごい）中のあるもののみならず、その文法や措辞法に、東西を結びつける連鎖のようなものを認める、と思ったからである。
　最近に至って「言語」に対する自分の好奇心を急激な加速度で増長せしめるに至った経路はあるいは一部の読者に興味があるかもしれないし、また自分が本分を忘れて、他人の門戸をうかがうような不倫をあえてするに至った事の申し訳にもいくぶんはなるかもしれないから一つの懺悔話（ざんげばなし）としてここにしるしてみよう。
　地球物理学上の近年の問題となっている陸塊の水平移動に関する学説、俗に大陸漂移論と称するものから見た日本陸地の成立、変化、ならびにこれに連関して問題となるべき陸地の昇降、地震、火山現象等を追究するに当たって、しばしば古い過去における水陸分布の状態と現在のそれとの異同が問題となり、その一つの参考資料としていろいろな土地の地名の意義が引き合いに出る場合がある。そこで本邦地名の問題に触れるとなれば、自然の勢いで、アイヌ語や朝鮮語による地名起原説を参照しなければならぬ事になる。そうなると問題は自然自然に推移して結局は日本語の成立問題にまでも多少は触れないわけには行かなくなるのである。
　そうかと言って、自分でこのような大問題をどうにかしようという非望を企てるわけにも行かないわけであるが、それでもただやみがたい好奇心から、余暇あるごとに少しずつ、だんだんに手近い隣接国民の語彙（ごい）を瞥見（べっけん）する事になり、それが次第次第に西漸していわゆる近東から東欧方面までも、きわめて皮相的ながらのぞいて見るような行きがかりになって来たのである。
　こういう素人遊戯（しろうとゆうぎ）――自分では真剣なつもりであっても、専門の学者の立場から見れば結局こういうよりほかはないであろう――にふけっている一方で、かねてから、これも道楽として、心がけている日本楽器の沿革に関する考証は自然に世界各地の楽器の比較に移って行く、その途中で、遠くかけ離れた異種民族の楽器が、その楽器としての本質においてのみならず、またその名称においても、一脈の連鎖によって互いにつながっているらしく見える現象に逢着（ほうちゃく）して、奇異の感に打たれる事もしばしばあった。もちろん楽器の原理は物理学的に普遍なものであるから、各国に同一な楽器のあるのは当然であり、また楽器の名称が往々擬音から生ずるとすれば、類似の名称のあるのは当然であると言って、簡単に片付けて投げ出してしまえばそれまでである。しかしそれで打ち切ってしまうのは少し危険であると思わせる理由がいろいろ他の方面から供給されるようである。
　少し唐突ではあるが地球上における蚯蚓（みみず）の分布を調べた学者の研究の結果によると、ある種の蚯蚓は、東は日本から海を越えて大陸に、欧亜大陸を横断して西はスペインの果てまで広がり、さらに驚くべき事には大西洋を渡って北米合衆国の東部にまでも分布されているのである。大陸移動説を唱えたウェーゲナーは、この事実をもってヨーロッパと北米大陸とが往昔連結していたという自説の証拠の一つとしてこれを引用しているくらいである。それはとにかく、あの運動遅鈍なみみずでさえ、同じ種族と考えられるものが、「現時の大洋」を越えてまでも広がっているという事実を一方に置いて考えてみる。もちろんこの蚯蚓の先祖と人間の先祖とどちらが古いかというような問題はあってもそれは別として、この事実はともかくも、過去の世界じゅうの人間の間の相互の交渉は、普通想像されているよりも、想像されうるであろうよりも、もう少し自由なものではなかったかという疑いを喚起させるには充分であろうと思う。
　世界じゅうの人間の元祖が一つであろうという事は単に確率論的の考察からもいちばん考えやすい事であるが、今ここで軽々しくそういう大問題に触れようとは思わない。ただ少なくも動物学上から見て同種な Homo Sapiens としての人間の世界の一部において任意の時代に発生した文化の産物のすべてのものが、時とともに拡散して行くのは、ちょうど水の中にたらした一滴のアルコホルの拡散して行く過程と、どこか類似したものであろう、という想像は、理論上それほど無稽（むけい）なものではあるまいと思われる。
　昔の詩人ルクレチウスは、物質の原子はちょうどアルファベットのようなもので、種々な言語が有限なアルファベットの組み合わせによって生ずるごとく、各種の物質がこれら原子の各種の組み合わせによって生ずると書き残したが、この考えは近世になって化学式というものによっていくらか科学的に実現された。今この考えを逆に持って行くとこんな考えも起こし得られる。すなわち、まず、言語、国語という一つの体系は若干の語根元素から組成されていると仮定する。次には、この元素が化合して種々の言語や文章が組成されているが、これらの間にはその化合分解の平衡に関するきわめて複雑な方則のようなものがあると想像する。なおこれらの元素は必ずしも不変なものではなくて、たとえば放射性（ラディオアクティヴ）物質のごとく、時とともに自然（スポンテニアス）に崩壊（ディスインテグレート）し変遷（トランスミュート）する可能性を持つものと想像する。それでかりに地球歴史のある一定の時期において、ある特別の地点において、特殊の国語が急に発生したと仮定すると、それはちょうど水中にアルコホルの一滴を投じたと同様に四方に向かって拡散（ディフュージョン）を始めるであろうと仮想される。すなわちその国語の語根のある一つだけを取って考えると、それはアルコホルの一分子のように、不規則にあちらこちらと人から人を伝わって、迂曲（うきょく）した径路を取りながらも、ともかくも、統計的には、その出発点から次第に遠く離れて行くであろう。もっとも、この際問題を複雑にするのは、物質分子の場合と異なり、言語の一分子は独立の存在として彷徨（ほうこう）するのでなく、その周囲に絶えず影響を与え、自分と同一なものを発生させて行く点にある。しかし一つの分子の通過したくらいでは、おそらくその径路への影響は短時間に消滅してしまうであろうと考え、ただ同種の分子が種々の径路を通ってある地域に到着し、ある時点におけるその密度が相当の大きさに達した場合にのみ、その地点の国語に固定的の影響を与えるであろうという、少し無理であるが、またややもっともらしい仮定を許容すれば、問題はある度までは、やはり物質分子の拡散に類したものとなるのである。
　かくのごとき仮定のもとに、ある分子が時間ｔにおいて、距離ｒと、それより dr だけ大きい距離との間の地帯に達するプロバビリティは
であり、中心から同時に出発した分子総数がＮであれば、この時点にこの地帯に来るものの数は NW(r, t)dr である。しかしこれらの分子が放射物質のように自然崩壊をするものとすれば、この数はｔについて指数函数的（しすうかんすうてき）に減じるので
であるとすべきであろう。さすれば距離ｒにおける密度は、これを 2πrdr で除したもので、これをσとすれば
で与えられる。
　もし中心から不断に供給が続けられていれば、これを時間ｔに対して積分する事になるであろう。また中心が空間的に分布されて存在すれば、さらに空間的の積分が必要になる事はもちろんである。
　このような考えを実際の場合に応用して具体的の数量的計算をする事は、今のところ、不可能であり、またしいてこれを遂行しても、その価値は疑わしいものである。しかし、ただ、以上の考察の中に含まれた根本の考えがいくぶんでも実際の問題に触れたところがあるとすれば、右にあげた数式によって代表された理想的過程の内容とその結果とは、またいくぶんか実際の言語の拡散過程、ならびに時間的空間的分布の片影を彷彿（ほうふつ）させるくらいのものはあるであろうと思われる。
　もしもこの考えがいくらか穏当である事を許容するとすれば、そこからいろいろな、消極的ではあるが、だいじな事がらが想定される。すなわちまず世界じゅうで互いに遠く隔たった二つの地点に互いに類似した言語が存在し、その中間にはその連鎖らしいものが見つからない場合があっても、それだけでは、それが必ず偶然の暗合であるとは断定されなくなる。またある甲地方の古い昔の言語が今でも存し、あるいは今はその地に消滅していて、その隣国民乙の間に現存しているという場合においても、それだけでその語が甲から乙に移入されたものだと推定する事はできなくなる。なんとならばそれはかつて甲から乙に移った事があったとしても、それが甲と前後して乙でも死滅し、ずっとあとで丙から乙に移ったかもしれないからである。そのほか分子論的拡散論において言われるようないろいろの事は言われるが、これを要するに、一つ一つの言語の分子を比べるだけでは、それだけでは歴史的の前後は決定し難いという消極的な結果になるのである。これはちょうど水中のアルコホル分子を一つ一つ捕える事ができたにしてもわれわれは到底その一つ一つの径路を判定し難いと同様である。
　しかし前の考察から一条の活路が示唆される。それは、約言すれば、同系言語の「統計的密度」の「勾配（こうばい）」（gradient）によって、その系の言語の拡散方向を推定するという方法である。
　前の算式によって示さるるごとき理想的の場合においては、一般に同種分子の密度の勾配は、ともかくも中心に対して放射的である。これはもちろん計算を待たずとも明白な事である。それでもしかりにアジア大陸のある地点からある種の分子が四方に拡散したとすれば、その系統あるいは同色の言語要素の密度は多少同心円形分布の形跡を生じてもよいわけである。たとえこの要素の等密度線がどのように変形しようとも、少なくも、その密度の傾度最大方向のトラジェクトリーを追跡して行けば、ついにはその源に到着、あるいは少なくも近づく事ができそうである。
　ただ第一に問題となるのは、いかなる標準によってそのいわゆる同系要素なるものを識別しうるかという事である。これはもちろん難問題である。しかし幸いにして従来の言語学者の努力の結果は、この方法を漸進近似法（Method of successive approximation）によって進めんとする際にまず試みとして置かるべき第一近似の資料を豊富に供給してくれるのである。
　この識別法を仮定すれば、次は密度の統計的計算が問題になる。前記の理想的の場合の「密度」が直接いかなる数に相応するかはこれもむつかしい問題であるが、少なくもその一つの計量（メジュアー）として、それそれの地方の国語中における、問題の語系要素の百分率を取ってみる事も一つの穏当な試験的方法であろうと考えられる。そしてこれは必ずしも不可能な事とは考えられない。
　もちろん語根は言語のすべてではない、語辞構成や措辞法もまた言語の要素として重要である。これらをいかにして「分子」に分析するかはかなりむつかしい問題ではあるが、少なくも原理の上からはそれも不可能な事とは思われないのである。
　以上のような漠然（ばくぜん）たる想像――もちろんこれは今のところただ一つの想像に過ぎない――に刺激されて、まず手近なマライ語の語彙（ごい）に目を通す事を試みた。そうしてこの国語と邦語との類似のはなはだしいのに驚かされた。自然現象や動植物の名称などはそれほどでもないが、形容詞と動詞において特に著しい類似のあるらしい事を感じた。おもしろい事には、今日わが国一般に行なわれているきわめて卑俗な言語や、日本各地の方言と肖似する現行マライ語も少なくない。また試みに古事記をひもといて古い日本語を当たってみると、たとえばその中の歌詞――最も古い語の保存されているらしい――に現われたむつかしい語彙などが、かなりにもっともらしく、都合よくマライ語で説明され、また古代神名や人名などにも、少なくも見かけの上でもっともらしく付会されるものが存外多いのに驚かされた。滑稽（こっけい）な例をあげれば稗田阿礼（ひえだのあれ）の名が「博覧強記の人」の意味にこじつけられたりした。また他の方面で最も自分の周囲の人々を愉快がらせたのは、かの大江山（おおえやま）の「酒顛童子（しゅてんどうじ）」が「恐ろしき悪魔」と訳されたりするのであった。これほど関係の深いようにわれわれ素人（しろうと）にさえ思われるものが、何ゆえに今日まで言語学者によって高唱されなかったかが不思議であるように思われた。現にある学者の書には、明らかにマライと邦語の関係はたいしたものでないと書いてある。一方朝鮮語やウラルアルタイ、チャムモンクメール、オセアニック等の語系との関係についての論文は往々われわれの目にも入ったが、正面からマライとの関係を論じて、そうしてそれが一般学界ひいては世人の注意をひくほどに至ったもののあった事は寡聞にしてまだ知らなかったのである。
　朝鮮語との語彙（ごい）の近似は、何人もいだくべき予期に反して案外に少ないもののようである。ウラルアルタイックとも、少なくも語彙の点ではそれほどでない事も論ぜられているようである。しかしマライはこの点についてはおそらく前二者に劣る事はなさそうに思われたのである。
　その後に Van Hinloopen Labberton が一九二五年のアジア協会学報に載せた論文を読んで、自分の素人流（しろうとりゅう）の対比がそれほど乱暴なものでなかった事を知ると同時に、外国の学者の間ではこれがかなり前から問題になっている事を知るに至った。また、Whymant という人の「日本語及び日本人の南洋起原説」というのにも出くわした。そしてその中で日本人というものがはなはだしく低能な幼稚なものとして取り扱われているのに不快を感じると同時にその説がそれほどの名論とも思われないのを奇妙に思ったりした。
　マライを手始めに、アイヌや、蒙古（もうこ）、シナ、台湾（たいわん）などと当たってみると、もちろんかなり関係のありそうな形跡は見えるが常識的に予期されるほどに密接とも思われないのをかえって不思議に思った。それから、ビルマや、タミール、シンガリースなどから、漸次西に向かって、ペルシア、アラビア、トルコ、エジプトへんをあさってみると、やはりいくらかの関係らしいものが認められると思った。ハンガリーやセルボクロアチアンからフィンランドまで行ってみても同様である。
　しかしだんだんにこの調子であさって行くと、おしまいにはギリシア、ラテンはもちろん現在行なわれている西欧諸国の語にもやはり同程度の類似が認められる。またかけ離れたアフリカへんやアイスランドまでも網の目を広げられる事になってしまうのである。
　具体的の例はこの序論においては省略するつもりであるが、ただ自分の意味を明らかにするために、試みに若干の例をあげると、たとえば、最も縁の遠そうな英語ですらも、しいてこじつけようと思えばかなりにこじつけられない事はない。すなわち
［＃ここから表組］
beat butu
laugh walahu
flat filattai
hollow hola
new nii
fat futo
easy yasasi
clean kilei
ill walui
rough araki
hard katai
angry ikari
anchor ikari
tray tarai
soot susu
mattress musiro
etc. etc.
［＃ここで表組終わり］
　この程度のもの、またもっと駄洒落（だじゃれ）らしいものなら、まだいくらでもありそうである。これらでも、歴史も何も考えずに、子音転訛（てんか）や同化や、字位転換や、最終子音消失やでなんとかかとか理屈をつければつくであろうし、また中には実際に因果の連鎖のあるものもあるであろう。
　もっと思い切って、たとえばアフリカへ飛んで Chikaranga の語彙（ごい）を当たると、ちょっと当たっただけで
［＃ここから表組］
象 zhou
魚 hove［＃「v」は下線（_）付き、181-表組2行目］
鳥 shiri
咽喉 huro
［＃ここで表組終わり］
などが見つかる。「象」の訓キサと似たのにはマライの gajah（サンスクリットからとある）があるが、ゾウといったようなのはずいぶん捜したがなかなか見当たりにくくて、それが、どうであろう、突然こんな意外な所に現われたのである。「魚」も同様であった。「鳥」はむしろアイヌの chiri に近いから妙である。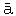土佐（とさ）で咽喉（のど）を切って自殺する事を「フロヲハネル」と言うが、この「フロ」が偶然出て来たのはずいぶん人を笑わせる。もっとも万一ことによると、これはアラビアの halq その他同系の語を通じて結局は西欧の gorge, throat, Hals などにもつながり、また一方たとえばベンガリの gal などを通してかなり東洋にも広がっているのかもしれないと想像される。もっと空想をたくましくすれば邦語のゴロなどというのも少しは怪しくなるくらいである。（鳥のアラビア語 tair. ［＃「t」は下点付き、182-6］咽喉（のど）のシナ語 hou lung）。
　こういう種類のではたとえばたっつけ袴（ばかま）のカルサンというのがインドへんから来ているかと思うと、イタリアにも類似の名が出て来たりするのである。（タミール語 Kalisan. イタリア語 Calzoni）。
　しかしこれらの例をあげたのは、決してこれらの語が邦語と因果的に関係しているという事を証明するためではなく、むしろただいかなる任意の二つの国語を取って比較しても、この種の類似がありうるものであるという事の例として取ったに過ぎない。それでたとえば、他方で「魚」や「鳥」の訓がシナ語や台湾語で説明されるとか、されないとかいう事は、ここでは問題にならないのである。
　ともかくも自分の皮相的な経験によると、いかなる国語の語彙（ごい）の比較でもあまりにおもしろい「発見」があり過ぎるような気がするので、これは少し考え方を変えなければならないという事に気がついた。そう思わせるもう一つの根拠に、ＡＢ両国語で互いに同じような音をもっていながら意味のほうでは明白になんの関係もないという例が、またかなりに多い。最も滑稽（こっけい）な例をあげるとフィンランド語では鶴（つる）が haikara であり、狼（おおかみ）が susi である。いかにこじつけたくても、フィンランドの鳥獣と東京の高襟（ハイカラ）や、江戸前の鮨（すし）とを連結すべき論理の糸は見つからない。しかしそうなると同じフィン語の狐（きつね）が kettu であり、小船が vene であり、樺（かば）が koivu であっても、これらの類似の前二者の類似との間の本質的の差を説明すべきよりどころがわからなくなるのである。
　浜の真砂（まさご）の中から桜貝を拾う子供のような好奇心の追究を一時中止して、やや冷静に立ち帰って考えてみると、これはむしろなんでもない事のようである、統計数学上の込み入った理論を持ち出すほどでなくとも、簡単なプロバビリティの考えから、少なくも原理の上からは、説明のつく事である、というふうに考えられて来た。
　まず試みに、子音にのみ注目するとする。そうしてＡの国語における子音の総数をｎとする。次に問題をできるだけ簡単にするためにＢ国語の子音をもこれと同数だとする。さらにいちばん簡単な場合を考えて、各子音がそれぞれ各国語に出現する頻度（ひんど）あるいは確率が一様で、皆νに等しいとすると、ν = 1/n ［＃「1/n」は分数］で均一になる。（これは少し乱暴に見えるかもしれないが、統計的方法では多くの場合近似の一法として許される事である。場合により頻度の著しく小さいものは省略する事もやってみてよい。）次に語彙（ごい）中で子音一つより成るもの、二つ、三つ、四つよりなるものというふうに分類する。そしてそれらのおのおのがＡＢ両国語に現われる確率をそれぞれ a1 a2 a3 …… b1 b2 b3 ……［＃アラビア数字はすべて下付き小文字］で示すとする。さすればＡ語のうちｉ個の子音より成るものの中のある一つを取って、それと同義の語がＢ語でも同じｉ個の子音の同順の排列からなるという事の確率は biνi［＃２文字目の「i」は下付き小文字、４文字目の「i」は上付き小文字］ であると考える事ができる。（無論Ａでｉが２のものを取る場合、Ｂでｉが２でないものはこの統計には入れない事にするのである）。ただしこれはＡ語一つに対するＢ語に同じｉ級のシノニムが他にないと仮定する場合で、もしシノニムがそれぞれ si［＃「i」は下付き小文字］ 個ずつあるとすればこの確率は si［＃「i」は下付き小文字］ 倍に増加する。もしこの上にメタセシスを許し、またＡ語の一子音に対すべきＢ語子音の転訛（てんか）範囲（はんい）を拡張すればこれはさらに増加する。それがいかに増加するかは計算しようと思えばされるはずのものである。しかしここでは最も簡単な場合として、同数シノニムというまでにとどめると結局ＡＢ両国（りょうこく）語彙（ごい）一般の比較によって得らるべき純偶然的一致の確率は、
で与えられるはずである。この中に出現するｓ、ａ、ｂ、νの各数はともかくも統計的になんとかして求められうる性質のものである。
　以上はできるだけ事がらを簡単に考えた考え方である。これ以上にだんだん試験的、近似的仮定を修正して、少しずつ実際の場合に近づけて行く事も、原理上からの困難はなく、ただ次第に計算が込み入るだけである。しかし、今のところ、あまりに込み入った計算では実用にならないから、できるならば簡単な形で進みたい。
　それで第一の試みとしては、まず前記のいちばん簡単な場合になるべく適合するように、材料のほうを選定し排列する事である。それはたとえば両国語の適当な語彙から比較に不適当な分子、たとえば本質的でないと思わるる接頭語、接尾語などを整理し（もちろんこれにはある仮定を要するが、それが tentative method として許容される事は、いわゆる精密科学においても同様である。そしてこの仮定には従来言語学者の苦心研究の結果が全部有効に利用されるはずである。）そうしてそれについて上記のａｂを出し、ｓは「近似的平均値」を推定して導入する。ここでいちばん困難なはＡＢのｎを同一に整理する事であるが、これにもいろいろの方法がある。たとえばＡ日本語とＢ英語の場合ならば、まず日本語のほうを、かりに「日本式ローマ字」で書く、しかして英語子音の「文字」の中で日本式にないものはかりに後者のどれかで「置換」する。たとえばｃやｑを皆ｋに直す類である。複子音も同様である。ｘなどは省いても、何かで置換しても統計の結果の値にはたいした影響は与えない事は明らかである。アラビアなどとなると、だいぶこの置換が困難な問題となるが、しかしたとえば喉音（こうおん）のあるものは半数だけｋかｇ、残り半数をｈで代用するというような試験的便法を取って第一歩を進める事もできる。（ここに統計的方法の長所があるとも言われる。）またたとえばマライ語の場合ならば ber, mer, per などのプレフィックスのｒを省いてみるとか、中間のngを省いてみるとかする事も試みてよいわけである。
　かくのごとき試験的（テンタティヴ）の整理によって、ともかくも両国語の子音がそれぞれかりに十四になったとする。次にかりに a1 a2 a3 a4 b1 b2 b3 b4［＃アラビア数字はすべて下付き小文字］ がいずれも１／４［＃「１／４」は分数］で a5 b5［＃「5」はすべて下付き小文字］ 以上は零とし、s1 s2 s3 s4［＃アラビア数字はすべて下付き小文字］ が平均皆４だと仮定すると
すなわち、指定のごとき比較によって、全然偶然から来る暗合の率が約二プロセントはできる事になる。
　しかし、上の仮定で明らかに最も不都合なのは、子音ただ一つをもつ語の割合をはなはだしく大きく見すぎた事である。これはシナ語の場合のほかには明らかに適用されない。
　それで、かりに、単子音語の確率を著しく小さいとして度外視し、なお次のごとく仮定する。
すなわちわずかに〇、四プロセント弱ぐらいに減じてしまうのである。
　なお、もしも、シノニムの数が、上記４の二倍であるとすれば、以上の百分値はやはり二倍になるだけであるから、このほうから結果の桁数（オーダー）に著しい影響は起こらない。
　次に特別な場合として、邦語をかな一つ一つに切り離し、その一つ一つと音韻の似た原語と同義のシナ文字を求め、それを接合して説明をするという、普通よくあるやり方をするとどうなるか。この場合は、a1 b1［＃「1」はすべて下付き小文字］ いずれも１で他は零となるから
しかるにシナでは異音類義の字が多いからこの s1［＃「1」は下付き小文字］ が大きくなりうる。かりに s1［＃「1」は下付き小文字］ を５とすると、三五、七プロセントという多数の暗合を見る事になる。これはこの種の方法による比較の価値を判断する際に参考になると思う。なおこの場合に同じ漢字の発音に対して、各地方的発音の異なるものを材料として、その中から都合のいいものを採るとなると s1［＃「1」は下付き小文字］ がさらにいっそうはなはだしく大きくなって、結局どうでもなるという事になり、かくのごとき比較の言語学上の価値はきわめて希薄になって来る事は明らかである。
　次に比較の標準を少し下げて、メタセシスを許容すると、Ｐの展開式のｉ項に※［＃「ｉ」の左側と下側を線で囲った記号、187-9］が乗ぜられる事になるが（ただし子音が皆異なるとして）、これでは少なくもｎがあまり小さくない限り、明らかに最後の結果の桁数（オーダー）に変化は起こらない。
　次に、子音転訛（てんか）を拡張して行くと、上記のｎが減少し、νが増加するから、これはＰに重大な影響を及ぼす事となる。かりに濁音を清音と同じにしたり、ｋとｈ、ｍとｂ、ｓとｔなどを同一視したりいろいろして行くと、独立したものの数ｎは僅々（きんきん）五つか六つになってしまう。従って最後のＰは著しく増大する。たとえば、ｎを５とすると
であるから a1 = b1 = 0; a2 = b2 = a3 = b3 = 4/10; a4 = b4 = 2/10［＃アルファベットに続くアラビア数字はすべて下付き小文字、「4/10」「2/10」は分数］ の場合でも、P = s×0.007744 となり、ｓが４ならば、約三、一％を得るわけである。すなわち、三分ぐらいの符合では偶然だか、偶然でないかわからない事になる。
　以上はもちろんかなりいろいろな無理な仮定のもとに行なった計算である。これを逐次修正して言語学者の要求に応ずるように近づけて行くことは必ずしも困難ではないが、ここではしばらくこれ以上に立ち入らない事にする。
　要するにこれは、表題にも掲げたとおり、比較言語学上における統計学的研究の可能性を暗示するための一つの試みに過ぎないのである。
　学者の中には、二つの国語の間の少数な語彙（ごい）の近似から、大胆に二つのものの因果関係を帰納せんとする人もあるようであり、また一方においてあまりに細心で潔癖なために、暗合の悪戯に欺かれる事を恐れてこの種の比較に面迫することを回避する人もあるかもしれない。自分にはこの二つの態度がいつまでも互いに別々に離れて相対しているという事が斯学（しがく）の進歩に有利であろうとは思われない。むしろ進んで、暗合的なものと因果的なものとを含めた全体のものを取って、何かの合理的な篩（ふるい）にかけて偶然的なものと必然的なものとを篩（ふる）い分ける事に努力したほうが有利ではあるまいか。そうして統計的に期待さるべき暗合の確率と、実際の統計的符合率とを対照して、因果関係の「濃度」を示すべき数値を定め、その値の比較的大なるものについて、さらに最初の仮定の再吟味を遂行し、その結果に基づいて修正された新たな仮定を設け、逐次かくのごとくしていわゆる漸近的近似法によって進行すれば、少なくも現在よりは、いくらか科学的に研究を進められはしないかと考えるのである。
　たとえば子音転訛（てんか）の方則のごときでも、独断的の考えを捨てて、可能なるものの中から甲乙丙……等の作業仮定を設けて、これらにそれぞれ相当するＰを算出し、また一方この仮定による実際の比較統計の符合の率を算出し、この両者を比較して、その結果から甲乙丙いずれが最も穏当であるかを決定すべきである。
　統計的方法の長所は、初めから偶然を認容してかかる点にある。いろいろな「間違い」や「杜撰（ずざん）」でさえも、最後の結果の桁数（オーダー）には影響しないというところにある。そして、関係要素の数が多くて、それら相互の交渉が複雑であればあるほど、かえってこの方法の妥当性がよくなるという点である。
　それで、この方法を真に有効ならしむるには、むしろあらゆる独断、偏見、臆説（おくせつ）をも初めから排する事なく、なるべくちがったものをことごとくひとまず取り入れて、すべての可能性を一つ一つ吟味しなければならない。軽々しい否定は早急な肯定よりもはるかに有害であるからである。これは実験的科学を研究する者に周知の事である。また往々にして忘却される事である。もっともこういうたんねんの吟味をするにはかなりの手数と時間を要する。それかと言って、いつまでもなんらかこの種の方法をとらなければ、独断と独断との間の討論の終結する見込みは立たないように思われるのである。いかにめんどうでも遂行すればするだけ、あともどりはしないであろうと信ずる。しかもそのほう専門の研究者の専門の仕事として見る時は、他の科学者、たとえば天文学者、物理学者、化学者などの仕事に比してそれほどにめんどうな仕事とは決して思われないのである。
　もちろん、これも他の科学の場合と全く同様に、初めからそううまくは行かないであろう。そうして、すべての可能なるものへの試みの「不可能」を「証明」し、抹殺（まっさつ）する事にのみ興味をもつ「批評家」の批評を受けなければなるまい。しかしあらゆる「精密科学」はその根底において、ちょうどかくのごとき方法を取って進んで来たものである。すべてがそのはじめは不精密なる経験の試験的整理を幾重となく折り返し繰り返し重ねて、漸進的に進んで来たものである。その昔、独断と畏怖（いふ）とが対峙（たいじ）していた間は今日の「科学」は存在しなかった。「自然」を実験室内に捕えきたってあらゆる稚拙な「試み」を「実験」の試練にかけて篩（ふる）い分けるという事、その判断の標準に「数値」を用いるという事によって、はじめて今日の科学が曙光（しょこう）を現わしたと思われる。もし古来の科学者が、「試み」なしの臆断（おくだん）を続けたり、「試み」の結果を判断する合理的の標準なしに任意の結論を試みたり、あるいは「試み」に伴なう怪我（けが）のチャンスを恐れて、だれも手を下す事をあえてしなかったら、現在のわれわれの自然界に関する知識と利用収穫は依然として復興期以前の状態で足踏みをしていたであろう。そしてまた現在の進歩した時代から見た時に幼稚に不完全に見えないものがいかなる初期の科学の部門に見いだされうるであろうか。
　余談はしばらくおいて、ＡＢ、ＡＣ、ＡＤ……の関係、なお念のために比較の主客を置換してＢＡ、ＣＡ、ＤＡ……の関係の濃度に対するだいたいの比較的の数値を定める事ができたとすれば、少なくもここにＡＢという一つの「鎖の輪」が、従来よりはやや科学的な根拠の上に仮設される。さすれば次には、前にＡについて行なったと同様の方法を、今度はＢについて行なうべきである。そうしてともかくも、ＢＣという、「次の輪」の見当をつける。順次かくのごとくして、できるならばまた、世界の各方面から出発して、同じようにして、それぞれの鎖を――もちろんそういう鎖が存在するとの作業仮設のもとに――たぐって行く。もし多くの人の信ずるであろうごとく、この数々の鎖が世界のどこかに自然と集合すれば簡単である。さすればその焦点に集中した要素をやや確かに把握（はあく）し得らるるから、今度は逆の順序によってこの焦点から発散し拡散した要素の各時代における空間的分布を験する事ができる、その時に至ってはじめて、この編の初めに出した拡散に関する数式がやや具体的の意義を持って現われて来るであろう。もっともそれはできるとしてもはなはだ遠い未来において始めて実現されうる事であろう。
　しかし上に考えた鎖はおそらく一点には集中しないであろう、それがどう食い違うか、そこに最も興味ある将来の問題の神秘の殿堂の扉（とびら）が遠望される。この殿堂への一つの細道、その扉を開くべき一つの鍵（かぎ）の、おぼろげな、しかも拙な言葉で表現された暗示としてのみ、この一編の正当な存在の意義を認容される事ができれば著者としてむしろ望外の幸いである。
　自分はできるだけ根拠なき臆断（おくだん）と推理を無視する空想を避けたつもりである。しかし行文の間に少しでも臆断のにおいがあればそれは不文の結果である。推理の誤謬（ごびゅう）や不備があればそれは不敏のいたすところである。このはなはだ僭越（せんえつ）と考えらるべき門外漢の一私案が、もし専門学者にとってなんらかの参考ともならば、著者としての喜びはこれに過ぎるものはない。
　思うにこの私案の第一歩の試みを最も有効に遂行するためには、おそらく言語学者と科学者との協力が必要ではないかと思われる。もしこの両者が共同し、その上に機械的の計算や統計を担当する助手の数人の力をかりることができれば、仕事はかなりおもしろく進行しそうに思われる。しかしこのほうがむしろおそらく夢のような空想であるかもしれない。

　（付記）　以上の考察においては、最もこの種の取り扱いに便宜だというだけの理由から、単に「語彙（ごい）」「単語」のみを問題として、語辞構成法や文法上の問題には少しも触れなかった。しかし自分は決して後者の比較の重要な事を無視しているのではない事を断わっておきたい。もっとも文法のごときものでも、これを数理的の問題として取り扱う事が必ずしも不可能とは思われない。事がらが、見方によってはある有限数の型式的要素の空間的排列の方式に関するものであると見る事ができるからである。輓近（ばんきん）の数学の種々な方面の異常な進歩はむしろいろいろな新しいこの方面の応用を暗示するようである。また「除外例」というもののある事から起こる困難は、統計的方法の利器によって、少なくもある度まで救われうる見込みがある。これについては、さらに、機会があったら、いくぶん具体的に考えを進めてみたいという希望をもっている。
　最後に誤解のないために断わっておく必要のあるのは、従来とても統計的のやり方はあるにはあるが、単に数をかぞえて多いとか少ないとかいうだけではなんらのほんとうの統計としての意味がないという事である。全体に対する実際の符合率が偶然による符合率に対する比のみが意味をもつ、ここではそれを問題にしたという事である。