日本から南洋へかけての火山の活動の時間分布を調べているうちに、火山の名前の中には互いによく
この統計の基礎的の材料として第一に必要なものは火山名の表である。しかしこの表を完全に作るということがかなりな難事業である。まずたくさんの山の中から火山を拾い出し、それを活火山と消火山に分類し、あるいは形態的にコニーデ、トロイデ、アスピーテ等に区別することは地質学者のほうで完成されているとしても、おのおのの山には多くの場合に二つ以上の名称がありまた一つの火山系の各峰がそれぞれ別々の名をもっているのをいかに取り扱うかの問題が起こる。
また火山の名が同時に郡の名や国の名であったりすることがしばしばある。その場合そのいずれが先であるかが問題となる。国郡のごとき行政区画のできるはるかに前から、火山の名が存し、それが顕著な目標として国郡名に適用されたであろうとは思われるが、これも確証することはむつかしい。
山の名の起原についてはそれぞれいろいろの伝説があり、また北海道の山名などではいかにももっともらしい解釈が一つ一つにつけられている。これをことごとく信用するとすれば自分の企てている統計的研究の結果が、できたとしても、それは言語学的に貢献することは
それで唯一の科学的方法はこれらのあらゆる不確実な伝説や付会説をひとまず全部無視して、そうして現在の山名そのものを採り、全く機械的に統計にかけることである。たとえば
完全な材料はなかなか急には得難いので、ここではまず最初の試みとして東京天文台編「理科年表」昭和五年版の「本邦のおもな火山」の表を採ることにする。これは現在の目的とはなんの関係なしに作られたものであるから、自分の勝手がきかないところに強みがある。これを採用するとした上で山名の読み方が問題となるが、これは「大日本地名辞書」により、そのほかには
さて Aso, Usu, Uns(z)en, Esan の四つを取ってみる。これはいずれも母音で始まり、次に子音で始まる
一般に母音で始まり次にいずれか任意の一つの子音の来る場合が火山の表中で何個あるかを数えてみる。この数を N(VC) で表わす。するとこの中である特定の一つの子音、たとえばSならSが出現するという事のプロバビリテーはいくらか。この確率は可能な子音の種類の数(Qとする)の逆数となる。それで全然偶然的暗合ならば現われるべきこの型の火山名の数nは N(VC)÷Q になるはずである。しかるに実際にはこの特定型のものがm個あるとする(アソの場合では m = 4 )。さすれば
R = 実際数m/偶然数n = mQ/N(VC)[#「実際数m/偶然数n」「mQ/N(VC)」は分数]
なる比が大きいほど暗合でないらしい、何か関係があるらしい確率が増すのである。少なくもm個のうちの若干は互いに関係がありそうだということになるであろう。もっとも厳密に言えばこのほかに日本語の特徴としてはこのような組み合わせの現われる一般的の確率を考慮に入れるべきであるが、これは容易でないからしばらく度外視する。子音数Qをどう取るかがかなりむつかしい問題になるが、「アソ」の場合は、かりにこれを9と取る。すなわち(k, g)(s, z)(t, d)(n)(p, b, h)(m, b, mb, np)(y)(r)(w)の9とする。また山名としては山・岳・島・登・ヌプリ・峰等の文字を引き去った残りだけを取り扱う事にする。ただし
まず歴史時代に噴火の記録のあるものだけについて見ると N(VC) = 8 である。(ただし硫黄、岩雄も iwo, iwao としてこの部分に算入する。すなわちわざと都合の悪いほうを選ぶのである。)さすれば R = 4×9÷8 = 4.5 となる。少し虫のよい取り方をして硫黄、岩雄を Yuwo, Yuwao と見て除けば N(VC) = 4 となり R = 9 となる。
次に消火山活火山をも合わせて取り扱う場合には、N'(VC) = 11 となり、R = 3.3 に減ずるが、硫黄・岩雄の頭がyなる子音だとして、このアソ型から除けば R = 5.1 となる。
次に Koma(
 ), Kampu, Kombu, Kamui を取れば m = 7 である。この場合は子音始まりで子音二つの場合として、一般の子音二つのものの数 N(CC) を求めると、消火山も入れてであるから N(CC) = 48 である。ここでも子音数をQとする偶然の確率は 1÷Q(Q-1)(ただし子音二つが異なるとして)であるから
), Kampu, Kombu, Kamui を取れば m = 7 である。この場合は子音始まりで子音二つの場合として、一般の子音二つのものの数 N(CC) を求めると、消火山も入れてであるから N(CC) = 48 である。ここでも子音数をQとする偶然の確率は 1÷Q(Q-1)(ただし子音二つが異なるとして)であるから
R = mQ(Q-1)/N(CC)[#「mQ(Q-1)/N(CC)」は分数]
Q = 9, m = 7, N = 48 であれば R = 10.5 となる。活火山だけだと m = 2 なる代わりに N = 14 となるので R = 10.3 でやはりほぼ同値となる。いずれにしても偶然の場合とはTurumi, Tarumai, Daruma の場合は、活火山だけだとタルマイ一つ、すなわち m = 1 で統計価値があまりに少ないから、消火山も入れて n = 3 の場合を考える。この場合は子音三つであってNの最多数な場合である。それでもしこの場合の数 N(CCC) を現在の表中の火山の総数に等しいと取れば、これは結果のRを少なくするほうの取り方であるからこれで得られたRが大きければ、ほんとうはもっと大きい事になる。それでかりにそうしてみる。さすればこの場合 N(CCC) = 167, m = 3 また子音三個の組み合わせの順列の数は 9×8×7 = 504 であるから、R = 3×504÷167 = 9.0 強となる。
鳥海山はトリノウミと言ったらしい形跡があるので、これも入れるとするとRはさらに四分の五倍だけに増すわけである。
次に問題になるのは F(H)uz(d, t)i, Hiuti, Kudy
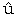 , K
, K du(sima), Kuti(no sima) の類である。KとHは日本語でもしばしば転化するからここではかりに同じと見て、次のような子音分類をする。すなわち(k, g, h, f)と(t, d, s, z)とを対立させると子音群数は Q = 7 となる。この場合 N(CC) = 48 であって m = 9(火山名略)であるから R = 7.6 となる。
du(sima), Kuti(no sima) の類である。KとHは日本語でもしばしば転化するからここではかりに同じと見て、次のような子音分類をする。すなわち(k, g, h, f)と(t, d, s, z)とを対立させると子音群数は Q = 7 となる。この場合 N(CC) = 48 であって m = 9(火山名略)であるから R = 7.6 となる。次には Yuwoo, Yuwao, Yufu を取り三つの「
以上の場合に得たRの価はいずれも1に対して相当多いものである。従って単なる偶然と見る事は少しむつかしく思われて来るのである。もちろんこれらが全部関係があるということは言われないが、これらのうち若干は連関しているであろうということを暗示するには充分であると思う。それでもし偶然でないとすれば以上にあげたような言語要素がいろいろな形で他の火山名の中にも現われていはしないかと思われる。また一方で同じ要素が南洋その他の方面にありはしないかと思われる。また南洋の言語中には従来の言語学者の説のごとく世界じゅうの言語が混合しているとすれば逆に遠い外国の意外のへんにも同じ要素が認められはしないかという疑いが起こる。それで試みに同型の疑いのある火山名を次ページの表に列挙して将来の参考に供しておきたいと思うのである。中には現在の形での意味がかなり明白だと思うのがあってもかりに除かないで採録しておくことにする。(外国火山名はおもにウォルフによる。)
アソ・アサマ型
| (本邦) | (外国) |
|
Aso Usu Unsen, Unzen Esan Unsy  (阿蘇の峰名) (阿蘇の峰名)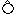 zy zy ( 〃 ) ( 〃 )Osore Rausu Rausi Rasyowa Gwassan Bessan(白山の一峰) Buson Nasu Kasa Kesamaru Asakusa Asitaka Asahi Usisir(千島の宇志知) Asama Aduma, Azuma Sanbe Sambon Sumon Samasana(火焼島) Shumshu Shimshir(千島の新知) Izuna, Iduna Udone |
Uson(カムチャツカ) Assongsong(マリアナ) Azuay(南米) Asososco(中米) Asur, Yasowa, Yosur, Yosua (ニューヘブリデス) Ossar(スマトラ) Azul(南米) Osorno( 〃 ) Izalco(中米) Lesson(ニューギニア) Lassen(カルフォルニア) Vesuvio(イタリア) Assatscha(カムチャツカ) Askja(アイスランド) Kara Aassam(スンダ) Pasaman Telamen(スマトラ) Pasema( 〃 ) Soemoe(スマトラ) Semeroe(ジャヴァ) Soembing( 〃 ) Semongkron( 〃 ) Gl 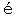 Samalanga(スマトラ) Samalanga(スマトラ)Samasate(中米) Saba(西インド) Etna(イタリア) (このほかの at-, ad- 型略す) |
第二表
ツルミ・タラ型
|
(本邦) |
(外国) |
|
Turumi Daruma Tarumai Torinoumi(鳥海) Chiripu Chiripoi Patarabe, Beritaribe Tara Tanra(済州島) Tori(鳥島) Tenry 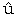 (白山絶頂) (白山絶頂)Adatara Hutara Kutara Madarao |
Tjerimai(ジャヴァ) Taroeb( 〃 ) Delamen( 〃 ) Sahen Daroeman(サンギ) Pasaman Telamen(スマトラ) Talla-ma-Kie 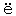 (ハルマヘラ) (ハルマヘラ)Tulabug(南米) Talima( 〃 ) Toliman(中米) Tolo(ハルマヘラ) Tara( 〃 ) Taal(タール) Talu(スンダ) Tauro(サロモン) Toro(南米) T 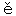 l l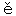 rep(ジャヴァ) rep(ジャヴァ)Teleki(東アフリカ) Tarakan(ハルマヘラ) Telok(スンダ) Tulik(アリウシャン) Telica(中米) Talang(スマトラ) Tarawera(ニュージーランド) Talasiquin(ズールー) Tultul(南米) Turrialba(中米, 白塔) Tjilering(ジャヴァ) |
このほかにまだコマ・カンプ型、クジウ型およびイワウ型があるがこれは今回は略し、他日の機会に譲ることとする。
この表中にヨーロッパやアメリカなどの火山が出て来るのを見て笑う人もあろうと思うが、しかし南洋語と欧州語との間の親族関係がかなり明らかにされている今日、日本だけが特別な箱入りの国土と考えるのはあまりにおかしい考えである。これについてはどうか私が先年「思想」に出した「比較言語学における統計的研究法の可能性について」を参照されたい。
また言語学者のほうからは、私の以上の扱い方が音韻転化の方則などを無視しているではないかという非難を受けるかと思う。しかしグリムの方則のような簡単
以上の調べの結果で、たとえば Aso, Usu, Esan, Uson, Asur, Osore, Ossar 等が意味の上で関係があると仮定すれば、これはいったい何を意味するかが問題となる。たとえば南洋エファテの Aso(燃える)Asua(煙る)サモアの Asu(煙)や、マレーの Asap(煙)(マレイでは火山は Gunong berasap すなわち煙山とも Gunong berapi 火山ともいう。Asap は Asama にも
コマ型、タラ型、フジ・クジウ型、ユワウ型についても同様なことが言われるのであるが、これらは後日さらに詳しく考えてみたいと思う。今回は紙数の制限もあるので以上の予備的概論にとどめ、ただ多少の見込みのありそうな一つの道を暗示するだけの意味でしるしたに過ぎない。従って意を尽くさない点のはなはだ多いのを遺憾とする。ともかくもかかる研究の対象としては火山の名が最も適当なものの一つであることは明らかであろう。たとえば川の名ではこういう方法は到底むつかしいと考えられる。最も顕著な特徴をもって原始民の心に最も強く訴えたであろうと思わるる地上の目標として火山にまさるものはないのである。しかしそういう目標に名前がつけられ、その名前がいよいよ固定してしまい、生き残りうるためには特別な条件が具足することが必要であると思われる。単に理屈がうまいとか、口調がいいとかいうだけでは決して長い時の試練に堪えないかと思われる。従来の地名の研究には私の知る限りこの必要条件の考察が少しも加わっていないではないかと思われる。この条件が何であるかについては他日また愚見を述べて学者の批評を仰ぎたいと思っている。
(昭和六年一月、郷土)