私はカントから出発する。併しカントの空間論に用いられる概念の間の関係は決して明晰ではない。之を予め纏めて見たいと思う。第一批判の「空間概念の形而上学的吟味」によれば空間は経験的概念でもなく又「物一般の関係に就いての比量的な所謂一般概念」でもない。概念は表象の Menge をその下に unter sich 含むものとは表象されるが決してそれをその内に in sich 含むものとは考えられない。然るに空間はその部分 R
 ume を in sich に含むものである。それ故空間は概念ではなくして直観でなければならぬ。処が又空間は「総ての外的直観の基礎に横たわるアプリオリな必然的な表象」であるから、空間はこの点から見て経験的な直観ではなくアプリオリな直観でなければならぬ。之を純粋直観と呼ぶ。次に吾々は空間内の対象なくしても空間を表象することは出来るが空間がないということは表象出来ない。即ち空間は「現象(之は外的現象と訂正すべきであろう)の可能の条件と見做される」のである。という意味は空間は物それ自身に属するものではなくして吾々の Gem
ume を in sich に含むものである。それ故空間は概念ではなくして直観でなければならぬ。処が又空間は「総ての外的直観の基礎に横たわるアプリオリな必然的な表象」であるから、空間はこの点から見て経験的な直観ではなくアプリオリな直観でなければならぬ。之を純粋直観と呼ぶ。次に吾々は空間内の対象なくしても空間を表象することは出来るが空間がないということは表象出来ない。即ち空間は「現象(之は外的現象と訂正すべきであろう)の可能の条件と見做される」のである。という意味は空間は物それ自身に属するものではなくして吾々の Gem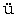 t の主観的な Beschaffenheit に属する、この意味に於て直観形式に属するものである。それ故吾々は茲に空間に就いて二つの概念内容を得た。純粋直観と直観形式。今この二つの概念内容がたとえ空間なる同一のものの概念内容であるとは云え、少くとも両者は概念内容としては直ちに同一ではないということは云うまでもない。それでは両者は斉しく空間なる同一なるものの概念内容であるということ以外に直接に如何なる関係に立つのであるか。カントは「空間概念の先験的吟味」に於て云う。空間はその概念がアプリオリに与えられたものと見られる時(形而上学的吟味の場合)と同じく、アプリオリな総合認識(幾何学の如き)を可能にする原理として見られる時も(先験的吟味の場合)まず第一に概念ではなくして直観でなければならぬ。そしてそれが凡ゆる知覚に先立つ点に於て純粋直観でなければならぬと。即ち之は前の場合に於ける純粋直観と同一のものを指す。処がこのような純粋直観が吾々の Gem
t の主観的な Beschaffenheit に属する、この意味に於て直観形式に属するものである。それ故吾々は茲に空間に就いて二つの概念内容を得た。純粋直観と直観形式。今この二つの概念内容がたとえ空間なる同一のものの概念内容であるとは云え、少くとも両者は概念内容としては直ちに同一ではないということは云うまでもない。それでは両者は斉しく空間なる同一なるものの概念内容であるということ以外に直接に如何なる関係に立つのであるか。カントは「空間概念の先験的吟味」に於て云う。空間はその概念がアプリオリに与えられたものと見られる時(形而上学的吟味の場合)と同じく、アプリオリな総合認識(幾何学の如き)を可能にする原理として見られる時も(先験的吟味の場合)まず第一に概念ではなくして直観でなければならぬ。そしてそれが凡ゆる知覚に先立つ点に於て純粋直観でなければならぬと。即ち之は前の場合に於ける純粋直観と同一のものを指す。処がこのような純粋直観が吾々の Gem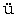 t に住み得る(dem Gem
t に住み得る(dem Gem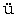 te beiwohnen)のはそれが主観の形式的な Beschaffenheit として即ち「外観一般の形式」として即ち直観形式として主観の内に座を占めることに依るのであるという。云い換えれば純粋直観が主観の内に座を占めると考えられる時それがとりも直さず直観形式なのである。それ故純粋直観が主観の内に座を占めると未だ考えられない間が所謂純粋直観であり、純粋直観が主観の内に座を占めると考えられる限りが直観形式である。さてこのことは純粋直観という概念内容に異った二つのものが同時に含まれていることを示している。即ち所謂純粋直観としての純粋直観と、直観形式としての純粋直観と。直観形式ではない処の純粋直観と、直観形式としての純粋直観とである。更に云い換えれば、前者に就いては形而上学的吟味の場合に於てのように純粋直観と直観形式とは区別され、後者に就いては両者は区別され得ないものである。そして事実この後の場合に相当するものを吾々は「感性論」の劈頭に発見する。それによれば現象内で感覚に対応するものを Materie と呼び「現象の多様が或る一定の関係に順序づけられる」ことを成り立たせるものを現象の Form と呼ぶ。処が感覚にぞくするものを少しも含まない表象を純粋と呼ぶのであるからかかる形式は「感性直観の純粋形式」と呼ばれる筈である。これは即ち直観形式である。処がかかる純粋形式に於て「現象の多様の総てが或る一定の関係に直観される」のである。故にかく直観するその理由によってこの直観形式は又それ自身純粋直観である、というのである。即ち直観形式即純粋直観ということとなる。かくして純粋直観が直観形式とは区別されながらそれと同時になお之と同一視されるという外見上の矛盾は、純粋直観という概念の異った二つの内容の区別と、而もこの異った二つの内容が或る何かの特殊な関係に従って同時に同じく純粋直観と呼ばれ得るということ、とを指し示すものに外ならない(私は以後直観形式と区別された方の純粋直観を第一のそれ、区別されない方を第二のそれと呼ぶ)。
te beiwohnen)のはそれが主観の形式的な Beschaffenheit として即ち「外観一般の形式」として即ち直観形式として主観の内に座を占めることに依るのであるという。云い換えれば純粋直観が主観の内に座を占めると考えられる時それがとりも直さず直観形式なのである。それ故純粋直観が主観の内に座を占めると未だ考えられない間が所謂純粋直観であり、純粋直観が主観の内に座を占めると考えられる限りが直観形式である。さてこのことは純粋直観という概念内容に異った二つのものが同時に含まれていることを示している。即ち所謂純粋直観としての純粋直観と、直観形式としての純粋直観と。直観形式ではない処の純粋直観と、直観形式としての純粋直観とである。更に云い換えれば、前者に就いては形而上学的吟味の場合に於てのように純粋直観と直観形式とは区別され、後者に就いては両者は区別され得ないものである。そして事実この後の場合に相当するものを吾々は「感性論」の劈頭に発見する。それによれば現象内で感覚に対応するものを Materie と呼び「現象の多様が或る一定の関係に順序づけられる」ことを成り立たせるものを現象の Form と呼ぶ。処が感覚にぞくするものを少しも含まない表象を純粋と呼ぶのであるからかかる形式は「感性直観の純粋形式」と呼ばれる筈である。これは即ち直観形式である。処がかかる純粋形式に於て「現象の多様の総てが或る一定の関係に直観される」のである。故にかく直観するその理由によってこの直観形式は又それ自身純粋直観である、というのである。即ち直観形式即純粋直観ということとなる。かくして純粋直観が直観形式とは区別されながらそれと同時になお之と同一視されるという外見上の矛盾は、純粋直観という概念の異った二つの内容の区別と、而もこの異った二つの内容が或る何かの特殊な関係に従って同時に同じく純粋直観と呼ばれ得るということ、とを指し示すものに外ならない(私は以後直観形式と区別された方の純粋直観を第一のそれ、区別されない方を第二のそれと呼ぶ)。それでは第一と第二の純粋直観のこの区別は実際には如何なるものとして現われるか。それを見るために私はカントの直観形式乃至純粋直観としての空間とは如何なるものと考えられるかを他の方面から検べて見る。空間を直観形式と云うにしてもカントの意味する処は実は框や箱のような frame-work であってはならないそれ自身力を働すものでなければならぬ。又それは Subjekt や Gem
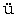 t の Beschaffenheit と云っても Subjekt や Gem
t の Beschaffenheit と云っても Subjekt や Gem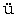 t の不変な構造 Organism とも云うべきものではないことも明らかである。直観形式とは直観の「基礎に横たわる」もの「現象の可能性」や感性の「制約」であるというのが最も当っているであろう。併し基礎と云い制約と云ってもそれが時間上何かに原因として或いは発達の歴史の上で先立つということでは勿論ない。この意味に於てそれは何かに論理的に先立つものと一応考えてよいであろう。併し論理的に先立つということが単に心理的に先立つのではないということだけを意味する限りこの言葉は正しいが、それが純粋に論理学的な意味に於て理由帰結の関係の理由を意味すると解釈することは今の場合全く意味がない。制約するものと制約されるものとの関係が論理の世界にあるという事はこの場合一般に無意味である。かく解釈された直観形式が例えば純粋直観であるなどと云うことは如何なる意味に於ても何処からも出て来る筈がないのであるから。それ故吾々に残される処は時間的な順序でもなく而かも所謂論理的な時間の順序でもない処の「基礎」又は「制約」でなければならぬ。それは之なくしては与えられた何物かが成立し得ないという意味に於ける限りの先験論理学的な予想であると云われるであろう。併しかく云ってもそれは直ちに制約そのものがロゴスの世界に属するということにはならない。なる程制約そのものはロゴスの世界にぞくし制約されるものの方はこのロゴスによって始めて成り立つものであると一応は考えられるでもあろう。併しロゴスから空間を如何に演繹することに努めるにしても得る処の終局のものは高々同時存在の形式に過ぎぬと思う。それは R
t の不変な構造 Organism とも云うべきものではないことも明らかである。直観形式とは直観の「基礎に横たわる」もの「現象の可能性」や感性の「制約」であるというのが最も当っているであろう。併し基礎と云い制約と云ってもそれが時間上何かに原因として或いは発達の歴史の上で先立つということでは勿論ない。この意味に於てそれは何かに論理的に先立つものと一応考えてよいであろう。併し論理的に先立つということが単に心理的に先立つのではないということだけを意味する限りこの言葉は正しいが、それが純粋に論理学的な意味に於て理由帰結の関係の理由を意味すると解釈することは今の場合全く意味がない。制約するものと制約されるものとの関係が論理の世界にあるという事はこの場合一般に無意味である。かく解釈された直観形式が例えば純粋直観であるなどと云うことは如何なる意味に於ても何処からも出て来る筈がないのであるから。それ故吾々に残される処は時間的な順序でもなく而かも所謂論理的な時間の順序でもない処の「基礎」又は「制約」でなければならぬ。それは之なくしては与えられた何物かが成立し得ないという意味に於ける限りの先験論理学的な予想であると云われるであろう。併しかく云ってもそれは直ちに制約そのものがロゴスの世界に属するということにはならない。なる程制約そのものはロゴスの世界にぞくし制約されるものの方はこのロゴスによって始めて成り立つものであると一応は考えられるでもあろう。併しロゴスから空間を如何に演繹することに努めるにしても得る処の終局のものは高々同時存在の形式に過ぎぬと思う。それは R umlichkeit とさえ云うことは出来ない。複素数が直ちに幾何学の平面であるのではない。無論同時存在が今の場合でも制約と呼ばれ得るということはそれ自身不当ではないであろう。併しそれは要するに思惟の形式であって今の場合に求められる直観の形式ではない。同時存在は云うまでもなく空間そのものではないのである。もしロゴスから空間そのもの(それは空間なる概念ではない)が演繹され得ないとすればかかる汎論理主義的解釈は今の場合には無用である。それでは所謂論理的基礎とか根拠とか予想とかと呼ばれるものはカントの空間の場合どう解釈すべきであるか。私は茲に空間意識は如何なるものであるかを多少立ち入って一般的に考えて見たい。Gesichtsraum とも云うように少くとも視覚は空間の意識を成り立たせている。視覚の対象を色と形に分かてば両者は互いの関係に於て全くその性質を異にしていると考えられる。云われる如く吾々は形のない色を表象することは出来ない。無論一定の形なくしても色を表象出来るであろうが形一般とも云うべき拡りなくしては不可能である。之に反して吾々は色なくしても拡りを表象し得るということが出来る。形はただ色と色との境界によってのみ成り立つにしてもその二つの色がすでに拡りの上で成り立っているのであるから色はただ拡りをして一定の形をとらしめるのに役立つだけである。拡りそのものは色には依存しない。今或る物体を視ると云う時恐らく色によって一定の形に限界された物体の表面を視るのであろうが、その場合吾々はフィヒテの云うように「表面を視ること」を直観しているのである、Sehen そのものを直観しているのである。この場合視られるものは物体の表面であるが直観されるものは物体の表面の純粋な形像であるということとなる。それが即ち空間である(Fichte, Bestimmung des Menschen.)。即ち純粋な形像(形、拡り)とは Sehen そのものの直観されたものである。赤の視覚は赤くないと云われるようにかかる純粋形像としての空間は色を含まない。視られた物体の表面はこの純粋な形の直観に色の感覚が加わったものと考えねばならぬ。かく云うと直観されるものは視覚であり又空間であるという不当な結論に来るかのように見えるが併し直観なるものの一般的な特質は直観するということが直ちに直観されるということに結び付く点になければならぬ。視覚が直観されると云うも直観するものが視覚の外に立つのではない、空間の直観は依然視覚の内になければならぬ、而もそれは単なる視覚を超えて直観するものでなければならぬ。視覚が直観されるとはかく直観することを意味する。そしてその対として空間が直観されるのに外ならない。又単に視覚が直観されるということから如何にして直ちにそれを空間の直観と云い得るかという疑問もあるかも知れないが、吾々は今空間を演繹しているのではなくして空間の直観としての特質を吟味しているにすぎない。空間は始めから予想されているのである。空間の直観はこのような根拠に於て感覚を超越し、Sehensakt そのものを直観することによって直観された空間を成立させる処の(何となれば直観するとは直観されることであるから)ものに外ならない。それ故これは単なる Anschauen ではなくして
umlichkeit とさえ云うことは出来ない。複素数が直ちに幾何学の平面であるのではない。無論同時存在が今の場合でも制約と呼ばれ得るということはそれ自身不当ではないであろう。併しそれは要するに思惟の形式であって今の場合に求められる直観の形式ではない。同時存在は云うまでもなく空間そのものではないのである。もしロゴスから空間そのもの(それは空間なる概念ではない)が演繹され得ないとすればかかる汎論理主義的解釈は今の場合には無用である。それでは所謂論理的基礎とか根拠とか予想とかと呼ばれるものはカントの空間の場合どう解釈すべきであるか。私は茲に空間意識は如何なるものであるかを多少立ち入って一般的に考えて見たい。Gesichtsraum とも云うように少くとも視覚は空間の意識を成り立たせている。視覚の対象を色と形に分かてば両者は互いの関係に於て全くその性質を異にしていると考えられる。云われる如く吾々は形のない色を表象することは出来ない。無論一定の形なくしても色を表象出来るであろうが形一般とも云うべき拡りなくしては不可能である。之に反して吾々は色なくしても拡りを表象し得るということが出来る。形はただ色と色との境界によってのみ成り立つにしてもその二つの色がすでに拡りの上で成り立っているのであるから色はただ拡りをして一定の形をとらしめるのに役立つだけである。拡りそのものは色には依存しない。今或る物体を視ると云う時恐らく色によって一定の形に限界された物体の表面を視るのであろうが、その場合吾々はフィヒテの云うように「表面を視ること」を直観しているのである、Sehen そのものを直観しているのである。この場合視られるものは物体の表面であるが直観されるものは物体の表面の純粋な形像であるということとなる。それが即ち空間である(Fichte, Bestimmung des Menschen.)。即ち純粋な形像(形、拡り)とは Sehen そのものの直観されたものである。赤の視覚は赤くないと云われるようにかかる純粋形像としての空間は色を含まない。視られた物体の表面はこの純粋な形の直観に色の感覚が加わったものと考えねばならぬ。かく云うと直観されるものは視覚であり又空間であるという不当な結論に来るかのように見えるが併し直観なるものの一般的な特質は直観するということが直ちに直観されるということに結び付く点になければならぬ。視覚が直観されると云うも直観するものが視覚の外に立つのではない、空間の直観は依然視覚の内になければならぬ、而もそれは単なる視覚を超えて直観するものでなければならぬ。視覚が直観されるとはかく直観することを意味する。そしてその対として空間が直観されるのに外ならない。又単に視覚が直観されるということから如何にして直ちにそれを空間の直観と云い得るかという疑問もあるかも知れないが、吾々は今空間を演繹しているのではなくして空間の直観としての特質を吟味しているにすぎない。空間は始めから予想されているのである。空間の直観はこのような根拠に於て感覚を超越し、Sehensakt そのものを直観することによって直観された空間を成立させる処の(何となれば直観するとは直観されることであるから)ものに外ならない。それ故これは単なる Anschauen ではなくして  ussere Anschauung(Fichte, Lotze 其の他)又は Hinschauen(Fichte)と呼ばれねばならぬ。而も空間直観のこの関係は云うまでもなく視覚には限られない。少くとも触覚にも共通でなければならぬ。併し元来この共通とは何を意味するか。それは視空間も触空間も結局同一の空間に落ち合わねばならぬということを意味する。もし同一の空間に落ち合わぬとすればそれは空間直観とは云うことが出来ない。何となれば空間をなお感覚乃至知覚と考える時にのみ心理学の教えるように二つの空間が異るものと考え得るのであるから。かく同一のものに落ち合うということは空間直観が感覚を超越するということから少くともその可能性を得なければならない。併し只それだけではそれがまだ実現されるには至らない。それが実現されるためには空間直観に規範性が予想されねばならぬ。空間の意識は単なる内在と解釈し尽すことは出来ない。それは意識を超えることの意識である。客観的実在の意識でなければならぬ。それは実在認識の規範でなければならぬ。空間の意識が単なる意識からしては演繹出来ない処に空間の radical な特質があると思う。空間は永遠に内在化すことの出来ない外界を成立せしめる規範である。客観界の唯一性は之によって始めて保証されるのである。この規範性によってあらゆる空間表象が唯一の空間直観に結び付くことが出来るのであると思う。そしてこの規範性によってのみ空間直観は原理上一般の直観と区別される。Hinschauen と云うも之に基くに外ならない。カントが空間に与えたアプリオリの性質は人も云うように正にこの規範性と解釈すべきである。かの「基礎」とか「制約」とかの真の意味も茲になければならぬと思う。併し茲に注意すべきことは、この規範性は空間がただ感覚を超越して作用そのものに基く処の空間直観というような現実の意識であったればこそ成り立つことが出来たものである。少くとも今の場合には例えば空間性というような規範が現実の意識を離れてそれ自身に成り立つというように考えることは絶対に出来ない。空間の規範性は正にそれが空間の直観であるという事情そのものに外ならないのである。規範そのものが空間の直観である。それが表象の規範であると共に又規範の表象でなければならぬ処に、空間が他の一切のものから区別される空間らしさがあるのである。空間は第一に直観でありその限り第二に規範である。
ussere Anschauung(Fichte, Lotze 其の他)又は Hinschauen(Fichte)と呼ばれねばならぬ。而も空間直観のこの関係は云うまでもなく視覚には限られない。少くとも触覚にも共通でなければならぬ。併し元来この共通とは何を意味するか。それは視空間も触空間も結局同一の空間に落ち合わねばならぬということを意味する。もし同一の空間に落ち合わぬとすればそれは空間直観とは云うことが出来ない。何となれば空間をなお感覚乃至知覚と考える時にのみ心理学の教えるように二つの空間が異るものと考え得るのであるから。かく同一のものに落ち合うということは空間直観が感覚を超越するということから少くともその可能性を得なければならない。併し只それだけではそれがまだ実現されるには至らない。それが実現されるためには空間直観に規範性が予想されねばならぬ。空間の意識は単なる内在と解釈し尽すことは出来ない。それは意識を超えることの意識である。客観的実在の意識でなければならぬ。それは実在認識の規範でなければならぬ。空間の意識が単なる意識からしては演繹出来ない処に空間の radical な特質があると思う。空間は永遠に内在化すことの出来ない外界を成立せしめる規範である。客観界の唯一性は之によって始めて保証されるのである。この規範性によってあらゆる空間表象が唯一の空間直観に結び付くことが出来るのであると思う。そしてこの規範性によってのみ空間直観は原理上一般の直観と区別される。Hinschauen と云うも之に基くに外ならない。カントが空間に与えたアプリオリの性質は人も云うように正にこの規範性と解釈すべきである。かの「基礎」とか「制約」とかの真の意味も茲になければならぬと思う。併し茲に注意すべきことは、この規範性は空間がただ感覚を超越して作用そのものに基く処の空間直観というような現実の意識であったればこそ成り立つことが出来たものである。少くとも今の場合には例えば空間性というような規範が現実の意識を離れてそれ自身に成り立つというように考えることは絶対に出来ない。空間の規範性は正にそれが空間の直観であるという事情そのものに外ならないのである。規範そのものが空間の直観である。それが表象の規範であると共に又規範の表象でなければならぬ処に、空間が他の一切のものから区別される空間らしさがあるのである。空間は第一に直観でありその限り第二に規範である。さてかくして第一に空間意識はかかる意味に於て空間直観であることを明らかにした上で吾々の始めの問題であったかの第一及び第二の純粋直観の区別を見よう。已に述べたように直観には一般に直観するものの方面と直観されるものの方面とが備わっていなければならぬ。従って空間直観には客観化されたものの側と未だ客観化されない主観の側とがなければならぬ。今第二の即ち直観形式である処の純粋直観はそれが直観の形式である以上そして直観が之なくしては成立しない以上この直観に或る一定の意味に於て先立つものでなければならぬ。然るに之は恰も前に述べた空間直観の未だ客観化されない側がもつ性質に外ならない。それ故第二の純粋直観とは直観する側面であり従って第一の純粋直観は直観される側面となる。事実カントは第一の純粋直観に関しては常に幾何学的に対象化された空間を例に引くのである。こう考えて始めて両者は空間直観のこのディアレクティッシュとも云うべき特質によって同時に同じく純粋直観と呼ばれる必然性があると云わねばならぬ。そしてかかる意味に於ける直観形式と純粋直観との対立を意識して来ることはとりも直さずカントがその感性論を離れてその「先験論理学」の空間論に這入って行くこととなる。
カントは「演繹」に於て次の如く云っている。「外的感性的なる直観の単なる形式である空間はまだ全く認識ではない。その空間は単にアプリオリな直観の多様を或る可能的な認識へ与えるに過ぎない。併し何かを例えば線を空間内に認識するためには私はその線を引いて見なければならぬ。かくて与えられた多様の一定の結合を総合的に成り立たせねばならぬ。かくてこの手続きの統一は同時に意識の統一(或る線の概念)である。そして之によって始めてオブヤェクト(一定の空間)が認識されるのである」と。之によれば始めに「まだ全く認識ではない」と云われた単なる形式としての空間は吾々の先の意味での直観形式であり、カントが之とは区別した処の「一定の空間」なるものは従って明らかに第一の意味での純粋直観に外ならぬと一応は考えられる。事実カントが「空間は単に感性の形式としてではなく直観自身として表象される」(Kritik der reinen Vernunft, 2 Aufl. S. 160)と云う時、この直観自身とは特に直観されたものを意味すると解さねばならぬ如く、前の「一定の空間」とは明らかに第一の意味での純粋直観に外ならぬと一応は考えられる。即ち茲にカントは私が先程指摘した様に第一の純粋直観と直観形式との対立に立つものと考えねばならぬ。然るにこの対立と共にカントは同時に夫に一つの転向を与えていると考えられる。というのはカントの言葉に従えば空間は「ある多様を含む処の直観自身として表象される、即ちこの直観内のこの多様の統一という規定を以てアプリオリに表象される」(S. 160)と云うが「直観自身として表象される」とは依然直観されるということ以外に正当な意味はないと思う。カントは直観的表象に統一するとも云っている。従って茲に直観自身として表象されるという意味での直観と直観自身とが再び区別されねばならぬ。前者は多様の統一という規定を持つに反して後者にはそれを持つということが考えられていない。後者は単に直観されたるもの即ち第一の意味での純粋直観であるに反して前者はカントの言葉を用いれば「多様を一つの直観的な表象に zusammenfassen する」処の統一という規定を備えた直観でなければならぬ。即ち前の場合にはもはや第一の意味での純粋直観と全く同一とは考えられない。カントは特に之を形式的直観と呼ぶのである。併しカントはこの形式的直観と純粋直観との異同は特にこれを言明してはいないように思われる。私はもう少し立ち入って茲を解釈して見よう。形式的直観が統一という性質を備えているということは如何なる意味であるか。夫は云うまでもなくこの統一によって形式的直観そのものが成り立っているということに外ならない。即ち形式直観が統一の結果であるということである。処がこの統一をば統一するものと統一されるものとの二つの分に解いて考えて見るとすれば、この場合統一されるものというのに相当するものはこの形式的直観ではない。何となれば形式的直観はすでに統一されたものであるから。従って求められたものは未だ統一されない処の直観に相当しなければならぬ。即ちそれは先の第一の純粋直観というの外はない。然るに明らかに単に統一するもの又は単に統一されたるものというものはない、成り立っているのは統一されたるものである。即ち単なる純粋直観なるものはない、あるものはただ純粋直観が統一された形式的直観のみである。それ故正しく云うならば形式的直観の統一によって始めて純粋直観が成り立つのである。云い換えれば第一の純粋直観は形式的直観のコンポーネントと考えられることによって始めて空間直観の面目を現わすものである。純粋直観とは実は形式的直観でなければならぬ。カント自身の云うように形式的直観の統一によって空間が直観として始めて「与えられる」のである(S. 161)。吾々は今純粋直観と直観形式との対立から出発したのであるが、純粋直観がかく形式的直観に帰するとすれば、それではかかる形式的直観とかの直観形式とは如何なる関係に立つか。「直観の形式は単なる多様を、之に反して形式的直観は表象の統一を与える」(S. 160)ものである。それ故形式的直観は単なる直観の形式以上のものと考えねばならぬであろう。而も「空間は対象として表象される時(それは実際幾何学で必要なことであるが)それは直観の単なる形式以上のものを含む」(同上)。之によって見れば形式的直観とは実はすでに対象化されたものであると見ねばならぬ。それでは形式的直観の未だ対象化されない処のものは何であるか。それが直観である以上かかるものは必ずなければならぬことである。それは何か。それは明らかにこの直観形式ではあり得ない。何となれば之によっては単なる多様が与えられるだけであるから。併しながら第一の純粋直観が先に述べた意味に於て形式的直観(対象化されたる)に帰する以上その対立たる直観形式も亦形式的直観(対象化されざる)に帰する外はない。直観形式というも実はこの意味での形式的直観に帰するものと考える外はない。単なる多様を与える直観の形式なるものはない、あるものは多様の統一即ち直観的表象への統一を与える直観形式のみである。それ故かくして純粋直観と直観形式との対立は対象化された形式的直観と未だ対象化されざる形式的直観との対立に移って来る。この移り行きはとりも直さずカントがその「演繹」から※[#下側の右ダブル引用符、U+201E、370-下-20]Analytik der Grunds
 tze“の空間論に移ることを意味するものであると思う。
tze“の空間論に移ることを意味するものであると思う。この対象化されたものと見るべき形式的直観のこの表象の統一はカントによれば「与えられたる直観一般の多様を範疇に従って根本的な意識に結合する統一に外ならない」(S. 161)。これは如何にして可能であるか。カントによればこの統一は「空間の諸概念 alle Begriffe」が始めて可能にされる処の Sinn には属さない或る一つの総合を予想している。即ちこの表象の統一の背後には或る一つの総合がなければならぬ。この総合を明らかにするものは「直観の公理」に外ならない。凡ゆる現象が経験的な意識(それは現実的な意識という意味であるが)にとり入れられるためには das Gleichartige の結合とこの同様なるものの多様の総合的な統一の意識に是非とも依らねばならぬ。処がこの同様なるものの多様の意識は直観に於ては量の概念である。然るに吾々は「どんな短い線と雖もそれを心の内で引く in Gedanken zu ziehen のでなければ、即ち一点から次第次第に凡ゆる部分を生産しそれによって始めて線という直観を示すことによらなければそれを表象することは出来ない」。吾々はこのように部分の表象が全体の表象を基けそれに先立つものを外延量と呼ぶ。それ故空間はかかる外延量に外ならない。直観の公理の「原理」に従えば「総ての直観は外延量」なのである。外延量として統一されたる直観は上に述べたような部分の順次総合によって可能となるのである。外延量として統一されたる空間の直観は対象化された統一を含む点から見てかの対象化された形式的直観でなければならぬ。然らばこの対象化された形式的直観を基けると考えられた部分の順次総合とは何か。カントによれば空間の意識に於てかく部分を順次に総合するものは produktive Einbildungskraft に外ならない。一般に現実意識を齎すものは実にこの生産的構想力である。生産的構想力が空間直観を成り立たせるレーゲルこそこの順次総合に外ならない。このレーゲルは空間の表象の統一そのものである。そしてこのレーゲルによって生じた Produkt 即ち「図式」としての図形の如きものこそかの対象化された形式的直観である。それ故生産的構想力のこの順次総合こそ正しくかの未だ対象化されない形式的直観に相当しなければならぬ。空間を単に客観的なものとしてのみは考えずに空間の具体的なる形式的直観と解する時以上の如く考えねばならぬのではないかと思う。対象化された形式的直観と未だ対象化されない形式的直観との対立は構想力としての形式的直観によって直接に結び付くのでなければならぬ。空間が直観である所以はカントに於てはかかる形式的直観として現われると思う。そして又形式的直観はすでに構想力と解釈されたのであるがカントによれば構想力は範疇へ結び付くものでなければならぬ筈である。構想力の順次総合のレーゲルとは構想力が範疇に従うことを意味するに外ならない。即ち形式的直観はその限りに於て範疇的と呼ばれることが出来る。然るに範疇とは人も云うように認識の規範ということに外ならない。形式的直観は規範的でなければならぬ。カントが空間に認めたアプリオリとは実はこの規範性に外ならない。直観空間は規範である。
カントの空間をば一応このように解釈出来るとして私は幾何学とこの直観空間との関係を多少立ち入って考えて見たいと思う。カントの識った幾何学は恐らく三次元のユークリッド幾何学であったと想像される。もとより空間の直観そのものがユークリッド的であるか或いは又未だ何等そのような規定を持たぬものであるかということに就いてカントの言葉を聴くことは出来ないであろう。併しカントによればユークリッド幾何学はかかる直観に基くものであり、而もユークリッド幾何学が唯一の幾何学であったと想像される以上、吾々はカントの考えた直観空間をユークリッド的であったと想像するのが自然であるであろう。それでは所謂非ユークリッド幾何学はそれがユークリッド幾何学と相容れないという理由からしてカントの直観空間に基くことは出来ないと云わねばならぬのではないか。事実この点に就いてカントの空間論に対する反駁は普通行なわれる処である。今カントの直観空間がユークリッド的であったと仮定し、且つそれ故にそれが非ユークリッド幾何学を基礎づけることが出来ぬであろうという批難に対して Medicus はカントの精神に従って弁護する(Kants transzendentale
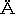 sthetik und Nichteuklidische Geometrien. Kantstudien 3.)。カントの空間は飽くまで現象又は経験の制約と解釈されるべきものである。それ故かかる制約としての空間がユークリッド的であるとか非ユークリッド的であるとかいうことは本来意味のないことと云わねばならぬ。空間のユークリッド的性質即ちその平面性は経験の必然的な制約として演繹されることは出来ない。それは空間の直観が経験から得た特徴に過ぎないものであり、従って必然的に妥当するものではなくして単に事実上妥当するものに外ならない。それは高々宇宙論上の価値以上のものを持つことは出来ない。空間とは平面的とも非平面的とも考えることの出来ぬ空間関係の原理なのである。この原理が空間関係それ自身としてユークリッド乃至非ユークリッド幾何学にその基礎を与えるのではあるが幾何学のかかる種々なる区別にも関らず空間的総合のこのような一般的法則そのものはあくまで一者であると考えられねばならぬ。併し勿論それにも関らず人々は直観の空間は平面的であると信じている。この信念に従って人々は非ユークリッド空間をも表象し得るのである。即ちユークリッド幾何学は他のすべての幾何学の規範としての意味を持ち従ってその平面的空間が直接に与えられたもののように見えるのである。併しこの規範的意味なるものも経験に由来する処の心理的で主観的なものに過ぎないのであるからそれは先験性とは別である。吾々は直観空間の平面性を信じるにしてもそれが非平面的であり得るという可能性を先験的に否定して了う理由は持たないと。今この結論の是非はともかくとしてその根拠にはなお困難がありはせぬかと思われる。空間を経験の制約、空間関係の原理と云うも、それは云うまでもなく単なる経験の制約ではなくして「空間」なる特殊の「経験の制約」であり、単なる原理ではなくして「空間関係」なる原理である。それゆえ空間に固有なものを引き去った一般的な「経験の制約」や「原理」の規定に就いて云々してもそれは空間と何の関わる処もない。吾々は空間が何故に経験の制約であり原理であるのかを知らねばならぬ。而もカントの立場に立てばすでに述べたように空間が形式的直観であったればこそ始めてそれを「経験の制約」とも「原理」とも考える理由が出て来るのに外ならない。もし形式的直観ではなくても「経験の制約」と考え得ると云うならばそうすれば空間はカント自身の考えた範疇と少しも異る処はなくなって了う。空間が直観に属することを(譬えそれが範疇への関係なくしては成り立たぬとしても)忘れる時空間は空虚な概念となって了わねばならぬ。カント自身「人間の認識の純粋な要素の研究に於て私は長日月の熟考の後始めて感性の純粋なる要素概念(空間と時間)と悟性のそれとを確実に区別し又引き離すことが出来た」(Prolegomena, § 39)と告白しているように空間を制約と考え原理と考えることとそれを直観に属すると考えることとが引き離せない処に空間の空間たる構成的な特質がなければならぬ。空間を飽くまで形式的直観と解釈出来るならば、これが先験的に平面的であるか或いは先験的に未だそうとは考えられないかということは一応の問題となり得ると思う。従ってその平面性が「必然的な制約」として演繹される可能性も一応は認めなければならぬであろう。無論かく云えば空間をなお素朴的に対象的に考えているからであると批難されるかも知れないが、併し先にも述べたように空間直観は直観するものと直観されたものとが直ちに結び付く処がなければならず従って直観すること即ち原理とも云うべき空間と客観的な空間とが直ちに結び付いていなければならぬ。直観されたものが必ずしも客観的では無いと云うかも知れないが併しそうすれば空間は内感と何の異る処もなくなって了う。空間はカントなどにも残っていると云われるように外界の框と考えられる点が何処かになければならぬ。ただこの框に内面的な力としての原理を発見し得ない時にのみ始めてそれは批難されねばならぬ思想となるのである。又メディクスは直観空間の平面性は吾々の心理的な信念であり経験に由る規範に過ぎないと云うが、かかる信念や規範が経験に由来するとは如何なる意味を持つか。此の意味を突きつめれば空間の平面性が経験によって証明されて来たということの外はない。然るに寧ろ私のこの論文そのものが結果するように経験によって証明された平面性は実は物理的空間のそれであって直観空間のそれではない。処が吾々は直観空間は平面的であると信じている。それ故この「信念」はもはや上の意味で経験的であり心理的であるのではない。従ってそれは直観空間そのものに固有な「信念」というの外はない。平面性のこの「信念」は直観空間の本質に属するものではないであろうか。かく考える時空間が先験的に平面的であるかどうかを問題とすることが愈々必要となって来る。そして事実カントの空間を平面的であると想像する理由がある以上、カントは非ユークリッド幾何学を基礎づけることは出来ないという批難は依然として繰り返えされそうである。
sthetik und Nichteuklidische Geometrien. Kantstudien 3.)。カントの空間は飽くまで現象又は経験の制約と解釈されるべきものである。それ故かかる制約としての空間がユークリッド的であるとか非ユークリッド的であるとかいうことは本来意味のないことと云わねばならぬ。空間のユークリッド的性質即ちその平面性は経験の必然的な制約として演繹されることは出来ない。それは空間の直観が経験から得た特徴に過ぎないものであり、従って必然的に妥当するものではなくして単に事実上妥当するものに外ならない。それは高々宇宙論上の価値以上のものを持つことは出来ない。空間とは平面的とも非平面的とも考えることの出来ぬ空間関係の原理なのである。この原理が空間関係それ自身としてユークリッド乃至非ユークリッド幾何学にその基礎を与えるのではあるが幾何学のかかる種々なる区別にも関らず空間的総合のこのような一般的法則そのものはあくまで一者であると考えられねばならぬ。併し勿論それにも関らず人々は直観の空間は平面的であると信じている。この信念に従って人々は非ユークリッド空間をも表象し得るのである。即ちユークリッド幾何学は他のすべての幾何学の規範としての意味を持ち従ってその平面的空間が直接に与えられたもののように見えるのである。併しこの規範的意味なるものも経験に由来する処の心理的で主観的なものに過ぎないのであるからそれは先験性とは別である。吾々は直観空間の平面性を信じるにしてもそれが非平面的であり得るという可能性を先験的に否定して了う理由は持たないと。今この結論の是非はともかくとしてその根拠にはなお困難がありはせぬかと思われる。空間を経験の制約、空間関係の原理と云うも、それは云うまでもなく単なる経験の制約ではなくして「空間」なる特殊の「経験の制約」であり、単なる原理ではなくして「空間関係」なる原理である。それゆえ空間に固有なものを引き去った一般的な「経験の制約」や「原理」の規定に就いて云々してもそれは空間と何の関わる処もない。吾々は空間が何故に経験の制約であり原理であるのかを知らねばならぬ。而もカントの立場に立てばすでに述べたように空間が形式的直観であったればこそ始めてそれを「経験の制約」とも「原理」とも考える理由が出て来るのに外ならない。もし形式的直観ではなくても「経験の制約」と考え得ると云うならばそうすれば空間はカント自身の考えた範疇と少しも異る処はなくなって了う。空間が直観に属することを(譬えそれが範疇への関係なくしては成り立たぬとしても)忘れる時空間は空虚な概念となって了わねばならぬ。カント自身「人間の認識の純粋な要素の研究に於て私は長日月の熟考の後始めて感性の純粋なる要素概念(空間と時間)と悟性のそれとを確実に区別し又引き離すことが出来た」(Prolegomena, § 39)と告白しているように空間を制約と考え原理と考えることとそれを直観に属すると考えることとが引き離せない処に空間の空間たる構成的な特質がなければならぬ。空間を飽くまで形式的直観と解釈出来るならば、これが先験的に平面的であるか或いは先験的に未だそうとは考えられないかということは一応の問題となり得ると思う。従ってその平面性が「必然的な制約」として演繹される可能性も一応は認めなければならぬであろう。無論かく云えば空間をなお素朴的に対象的に考えているからであると批難されるかも知れないが、併し先にも述べたように空間直観は直観するものと直観されたものとが直ちに結び付く処がなければならず従って直観すること即ち原理とも云うべき空間と客観的な空間とが直ちに結び付いていなければならぬ。直観されたものが必ずしも客観的では無いと云うかも知れないが併しそうすれば空間は内感と何の異る処もなくなって了う。空間はカントなどにも残っていると云われるように外界の框と考えられる点が何処かになければならぬ。ただこの框に内面的な力としての原理を発見し得ない時にのみ始めてそれは批難されねばならぬ思想となるのである。又メディクスは直観空間の平面性は吾々の心理的な信念であり経験に由る規範に過ぎないと云うが、かかる信念や規範が経験に由来するとは如何なる意味を持つか。此の意味を突きつめれば空間の平面性が経験によって証明されて来たということの外はない。然るに寧ろ私のこの論文そのものが結果するように経験によって証明された平面性は実は物理的空間のそれであって直観空間のそれではない。処が吾々は直観空間は平面的であると信じている。それ故この「信念」はもはや上の意味で経験的であり心理的であるのではない。従ってそれは直観空間そのものに固有な「信念」というの外はない。平面性のこの「信念」は直観空間の本質に属するものではないであろうか。かく考える時空間が先験的に平面的であるかどうかを問題とすることが愈々必要となって来る。そして事実カントの空間を平面的であると想像する理由がある以上、カントは非ユークリッド幾何学を基礎づけることは出来ないという批難は依然として繰り返えされそうである。併し元来直観空間なるものは果してユークリッド的であるのか。もしそうとすれば如何なる意味に於てそうなのであるか。O. Becker(Beitr
 ge zur ph
ge zur ph nomenologischen Begr
nomenologischen Begr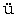 ndung der Geometrie und ihren physikalischen Anwendungen, Jahrbuch
ndung der Geometrie und ihren physikalischen Anwendungen, Jahrbuch 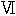 )は現象学的に次の三種の空間表象を区別する。第一 pr
)は現象学的に次の三種の空間表象を区別する。第一 pr spatiale od. Ausbreitungsfelder は視触聴の領野と眼筋及び触官の運動による領野とを現わし、第二 orientierter Raum は自己と外界との関係に於て成り立ち深さを持つ。この空間に於ては自己という中心点が特異点となるのであるが此の特異性が反覆される時第三の homogener Raum となると云う。吾々の所謂直観空間はこの第三のものの外にはないことは明らかである。さてベッカーはユークリッド的性質を空間曲率の値Kが零であることとその結合 Connexus が無限 offen(一元的に einfach)であることとに区別する(結合とは例えば空間的形像の面が縁を持つとか、持たぬとか、又は閉線を幾回旋して形像が二つに離れるか――結合度――などを取り扱う位置解析 Analysis situs, Topologie の根本概念である。恰も空間曲率が計量幾何学の根本概念であるように)。第三の等質的空間はまずK=0でなければならぬ。何となれば第一にかの orientierter Raum と等質的空間とを区別するものと考えられたかの反覆が可能であるためには合目的移動(剛体の運動)の群は Untergruppe として推移 Translation の群を含むことが必要であり、従ってリーの云うようにK=0であることが必然である。第二に等質的空間は合同な多数の形像に区画されることが出来る(例えば空間を同一の大きさの球と、球と球との間に出来る一定の形の多数の隙とによって満すことが出来る(Einstein, Geometrie und Erfahrung 等参照)。然るにK=0である時之は不可能であろう。第三に此の空間に於ては相似に関する命題が成り立ち又位置によって方向は変らない。このことは間接にK=0であることを証明している。それ故等質的空間の曲率は零でなければならぬ。次に等質的空間は Principium individuationis の一つに外ならぬのであるから周期性 Periodizit
spatiale od. Ausbreitungsfelder は視触聴の領野と眼筋及び触官の運動による領野とを現わし、第二 orientierter Raum は自己と外界との関係に於て成り立ち深さを持つ。この空間に於ては自己という中心点が特異点となるのであるが此の特異性が反覆される時第三の homogener Raum となると云う。吾々の所謂直観空間はこの第三のものの外にはないことは明らかである。さてベッカーはユークリッド的性質を空間曲率の値Kが零であることとその結合 Connexus が無限 offen(一元的に einfach)であることとに区別する(結合とは例えば空間的形像の面が縁を持つとか、持たぬとか、又は閉線を幾回旋して形像が二つに離れるか――結合度――などを取り扱う位置解析 Analysis situs, Topologie の根本概念である。恰も空間曲率が計量幾何学の根本概念であるように)。第三の等質的空間はまずK=0でなければならぬ。何となれば第一にかの orientierter Raum と等質的空間とを区別するものと考えられたかの反覆が可能であるためには合目的移動(剛体の運動)の群は Untergruppe として推移 Translation の群を含むことが必要であり、従ってリーの云うようにK=0であることが必然である。第二に等質的空間は合同な多数の形像に区画されることが出来る(例えば空間を同一の大きさの球と、球と球との間に出来る一定の形の多数の隙とによって満すことが出来る(Einstein, Geometrie und Erfahrung 等参照)。然るにK=0である時之は不可能であろう。第三に此の空間に於ては相似に関する命題が成り立ち又位置によって方向は変らない。このことは間接にK=0であることを証明している。それ故等質的空間の曲率は零でなければならぬ。次に等質的空間は Principium individuationis の一つに外ならぬのであるから周期性 Periodizit t(先の結合度と考えればよい)のような空間内容の自由を制限する合法則性を持つものではない。「それ故ユークリッド的計量を予想する時非周期的なる(即ち周期を除外もせず又それを与えもしない)統一形式が択ばれねばならぬ。それは即ちユークリッド空間の一元的に無限な結合である」。かくして等質的空間は無限 offen であるという。それ故直観空間はユークリッド的でなければならぬように見える。併しながら相対性原理などが非ユークリッド空間の存在即ち空間直観に於けるその妥当を要求するとすれば吾々は空間直観がユークリッド的であると同時に非ユークリッド的であるという矛盾に撞着することとなる。この矛盾は如何にして避けられるか。ベッカーは茲に空間の Konstitution とその Struktur とを区別し前者による Phantomraum なる直観空間はユークリッド的であるが後者による計量的空間は非ユークリッド的であり得るのであると説く(同上 S. 151)。計量乃至測定は現象学的にかの第二の orientierter Raum に基くが故に第三の等質空間なる直観空間は計量的空間と矛盾するものではないという。併し吾々が測定するとは単に眼で測る(それは orientierter Raum に於て応わしいことであるが)のではない、それは物理学的に量を決定するということに外ならない。然るに物理学的に量を決定するのは所謂等質的空間に干与して始めて可能となることである。空間の構造と雖も等質的空間の構成の上に立たねばならぬであろう。構造と構成とは二つの立場ではなくて一つの立場に於ける規定の段階の区別であると思う。それ故矛盾はこの区別によっては除かれされない。
t(先の結合度と考えればよい)のような空間内容の自由を制限する合法則性を持つものではない。「それ故ユークリッド的計量を予想する時非周期的なる(即ち周期を除外もせず又それを与えもしない)統一形式が択ばれねばならぬ。それは即ちユークリッド空間の一元的に無限な結合である」。かくして等質的空間は無限 offen であるという。それ故直観空間はユークリッド的でなければならぬように見える。併しながら相対性原理などが非ユークリッド空間の存在即ち空間直観に於けるその妥当を要求するとすれば吾々は空間直観がユークリッド的であると同時に非ユークリッド的であるという矛盾に撞着することとなる。この矛盾は如何にして避けられるか。ベッカーは茲に空間の Konstitution とその Struktur とを区別し前者による Phantomraum なる直観空間はユークリッド的であるが後者による計量的空間は非ユークリッド的であり得るのであると説く(同上 S. 151)。計量乃至測定は現象学的にかの第二の orientierter Raum に基くが故に第三の等質空間なる直観空間は計量的空間と矛盾するものではないという。併し吾々が測定するとは単に眼で測る(それは orientierter Raum に於て応わしいことであるが)のではない、それは物理学的に量を決定するということに外ならない。然るに物理学的に量を決定するのは所謂等質的空間に干与して始めて可能となることである。空間の構造と雖も等質的空間の構成の上に立たねばならぬであろう。構造と構成とは二つの立場ではなくて一つの立場に於ける規定の段階の区別であると思う。それ故矛盾はこの区別によっては除かれされない。ユークリッド空間と考えられた直観空間は無限 offen であるというがそれは実は週期性即ち結合からの独立を意味する。従ってそれは無限 offen とも有限 geschlossen とも考えられないと云わねばならぬ。このことは曲率に就いても云われはしないか。即ち直観空間はK=0でもなく又K≠0でもないと。何となれば元来空間その者の結合が問題となり得るのはただ空間の曲率に基くと考えられる限りに於てであり、空間そのものの結合もこの意味に於て計量的であると云わねばならなくなって来るから。私はこの点を追求して行く。直観空間の内面を最も直截に指摘したものはロッツェであると思う。ロッツェに於て直観空間は幾何学を基礎づけるものと考えられる。「線に就いて之を他と比較することによって吾々は長さと方向とを区別するが、両者に関する最も簡単な命題と雖も直観から学ぶのでないならば決して成立するものではない」(Metaphysik, S. 223―4)。幾何学に於ける総合判断は空間の直観によってのみ可能である。然らばロッツェの直観空間とは如何なるものか。線の形に於て直観された二つの要素間の関係rと、角の形に於てかかる二つのr間の関係wとは結合して吾々の直観空間をなすのであるが、此のrとwとが吾々の直観空間に於てとは異った結合をなす時成り立つと想像される所謂 Raumoid なるものは元来あり得ないものである(同上 S. 241)。即ち直観空間は唯一でなければならぬ。次に吾々は直線を曲線の極限と考え得ると云うが「その規定と計量とに当って何等か直線の直観を用いることなくしてはこの曲線の系列を作ることは出来ない」(同上 S. 246)。無限大の直径を持つ円として回帰し得るような直線とは論理的野蛮に過ぎぬ。平行線が永久に交らないということを逆にして平行線は無限遠点で交わると云い換えることは許されない。吾々は論証によって平行線の問題を決定することは出来ない。何となれば直観に対しては問題が起きる理由は全くないのであるから。平行線の存在は「直観の完全に明晰な事実」に基くのであるから、もし物理的現象に於て三角形の内角の和が二直角を離れるような場合が生じたとすれば、その場合にはそこに特殊の物理的な原因が存在して光線をば曲げたのであると吾々は解釈せねばならぬ。そして空間関係そのものは飽くまで不変であらねばならぬ(同上 S. 246―9)、即ち直観空間はユークリッド的と考えられる。併しロッツェによれば直線に対して曲線が考えられる時、それを可能ならしめる原理が直観空間の直線性として働く処のものである。直観空間のユークリッド的性質とはとりも直さずこの直線性の原理に外ならない。それではかかる直線性は何と考えるべきであるか。普通直線は曲率を持たぬと云われるのであるが私はこれを「曲率がない」ということと「曲率が零である」ということとの二つに区別する必要があると思う。吾々は射影幾何学には曲率がないと云い、計量幾何学には曲率があるという。そして後者の内ユークリッド幾何学に於てのみ曲率が零であると考える。それ故以上の区別は単なる言葉の分類ではない。直線が原理であると云う時、それは茲に曲率が考えられていないということ、即ち曲率がないということを意味するに外ならないと思う。何となれば零も一つの数と考えられる以上曲率が零であるという場合はそれが零でないという場合と対等の位置にある筈であり、従って前者が後者を基ける原理となるというようなことは零に特殊の意味を与えない限りこれからは出て来ようのないことなのであるから。直線性が原理であるとは曲率が零であるという特殊の場合を意味するのではなくして曲率がないということでなければならぬ。非ユークリッド幾何学に於ては所謂その直線と雖も曲率を持つのであるが、それにも関らず直線は矢張り一義的に他の曲線と区別されるということは直線性が曲率に依存しないということを意味するのではないであろうか。原理としての直線性は凡ゆる幾何学に一貫する原理であると思う。ポアンカレが射影幾何学は直線を予想し直線は計量に基くが故に射影幾何学も量的であるというが(Derni
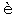 res Pens
res Pens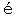 es, p. 58[#「Derni
es, p. 58[#「Derni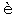 res Pens
res Pens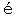 es, p. 58」は底本では「Derni
es, p. 58」は底本では「Derni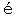 res Pens
res Pens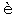 es, p. 58」])、元来射影幾何学に於てはこのような計量に基く直線はない。単なる線で充分である。而もポアンカレをして云わしめたように吾々はこの線を特に曲線と考える理由を持つことは出来ない、即ちなおある意味で線を直線と考えねばならぬ。量的直線と質的直線とが区別されねばならぬ。直線性の原理は正にこの質的直線によって現わされる。射影幾何学は質的なのである。それ故ロッツェの直観空間を立ち入って追求して見れば、直観空間は質的にユークリッド的であると云い得ると思う。そして非ユークリッド性なるものはK≠0という量的な規定なのであるから之は決して質的なユークリッド性とは矛盾するものではないということになるであろう。ヨーナス、コーンのようにユークリッド空間の先験性を主張する時(J. Cohn, Voraussetzungen und Ziele des Erkennens, S. 249)このように質と量とを区別してユークリッド空間は質的に先験的となるというならばそれは一層明らかとなるであろう。カントの空間をユークリッド的と解するならばそれをかかる質的平面性(直線性)と解することが出来る。そしてかく解してのみ吾々は空間の直観の質的な特質を
es, p. 58」])、元来射影幾何学に於てはこのような計量に基く直線はない。単なる線で充分である。而もポアンカレをして云わしめたように吾々はこの線を特に曲線と考える理由を持つことは出来ない、即ちなおある意味で線を直線と考えねばならぬ。量的直線と質的直線とが区別されねばならぬ。直線性の原理は正にこの質的直線によって現わされる。射影幾何学は質的なのである。それ故ロッツェの直観空間を立ち入って追求して見れば、直観空間は質的にユークリッド的であると云い得ると思う。そして非ユークリッド性なるものはK≠0という量的な規定なのであるから之は決して質的なユークリッド性とは矛盾するものではないということになるであろう。ヨーナス、コーンのようにユークリッド空間の先験性を主張する時(J. Cohn, Voraussetzungen und Ziele des Erkennens, S. 249)このように質と量とを区別してユークリッド空間は質的に先験的となるというならばそれは一層明らかとなるであろう。カントの空間をユークリッド的と解するならばそれをかかる質的平面性(直線性)と解することが出来る。そしてかく解してのみ吾々は空間の直観の質的な特質を平面性に就いて以上のように考えて見たがそれでは三次元に就いてはどう考えられるか。カントは空間の三次元を必然的なものとして幾何学の命題の一つにさえ数えている。それではカントの空間はn次元の幾何学を基礎づけることは出来ないのであるか。メディクスは平面性に就いてと同じく茲でも空間の三次元性は経験の必然的制約として演繹されるものではなく単に事実上そうあるに過ぎないのであるからこの点に就いてもカントに何等困難はないと弁護する。併し直観空間の三次元性はその平面性に較べてよほど「疑い得ない」ことである(上掲論文)。処がすでに述べたようにカントの空間が直観と考えられねばならぬのであるからこの「疑い得ない」ことがこの直観の規定として一応顧みられなければならなくなる。勿論それは理性的な必然性は持たぬであろう。空間の次元が何故に3でなければならぬかは理性の少しも教えない処である。その意味に於て経験の必然的な制約ではないであろう。併しかく考えられるものは実は空間そのものではなくして高々空間性に過ぎない。空間性には三次元であるべき理性必然性はないかも知れない、併し空間は直覚上是非とも三次元でなければならぬ。カントも考えたようにそれは「必然的」と云わねばならぬ。この必然性があって始めて直観空間が成り立つと云わねばならぬ。そしてこの直観空間故に空間が経験の制約と云われる理由も生じて来るのである。直観空間の三次元性の必然性を説く者は再びロッツェである。ヘルムホルツが、もし二次元の意識しか持ち得ない処の而も吾々と同じく英知的な生物があるとすればその生物の意識する空間はリーマン幾何学平面に相当するユークリッド空間の球面のようなものであり得るだろう(Popul
 re wissenschaftliche Vortr
re wissenschaftliche Vortr ge
ge 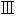 )と説いたが、ロッツェは之を反駁して二次元の意識しか持たぬ生物なるものは成り立たないと云う。この生物が球面の一点Aを出て経度に従って球面を一周すると考える時、たとえ先のAに帰ったとしてもこの生物は之を如何にして前のAと同一な点と知ることが出来るか。ただ全く同様なAなる感覚が再び繰り返すのであると思うだけであろう。もし空間関係を意識しているとすればそれは無限に延長した直線に於て一定の間隔を隔てて同一の事情Aが起こって行くというに過ぎないであろう。併しもし仮に同一のAなる点に帰ったということを何かの手段で知り得るならばこの生物は直線という概念に矛盾を発見する筈である。というのはロッツェによれば直線とは距離に外ならぬのであるから、この場合最大の距離が距離のないことを意味することとなる。生物はそれ故知覚に於てはともかく、論理的にはこの矛盾を避けることを強要される。従って空間の三次元性を予想することを強要される。即ちもし生物が空間表象を持つならばその持つと仮定された二次元は必然的に三次元に拡張されねばならぬと(Metaphysik, S. 249―252)。併し球面はリーマン空間の平面そのものではなくして既に述べたようにそのユークリッド空間に於ける表現に過ぎない。ロッツェは表現を空間そのものと見誤っているのであるからこの批難は批難そのものとしては当っていないと云わねばならぬ。併しロッツェの云い現わす処は直観空間が必然的に三次元でなければならぬということに外ならない。ロッツェに従えば英知的生物がこのようにして二次元から三次元に移るべく余儀なくされると同時に之を遂行し得るのであるが、同様にして吾々が三次元から四次元に移るということは云われない。何となれば二次元から三次元に移る必然性は一つの矛盾に由来したのであるが吾々は三次元に於てそのような矛盾は発見出来ない、且又吾々は四次元の直観を事実持つことが出来ないのであるから(同上 S. 252―257)。直観空間は三次元的でなければならぬであろう。カントの空間が直観であることを承認する限りたとえ空間が範疇へ結び付いた構想力によって成り立つと云ってもそれをば直観の規定であるこの三次元性を脱したものと考えてよい理由は何処にもない。空間は範疇へ結び付くにしても範疇そのものではない。範疇に従いながら(den kategorien gem
)と説いたが、ロッツェは之を反駁して二次元の意識しか持たぬ生物なるものは成り立たないと云う。この生物が球面の一点Aを出て経度に従って球面を一周すると考える時、たとえ先のAに帰ったとしてもこの生物は之を如何にして前のAと同一な点と知ることが出来るか。ただ全く同様なAなる感覚が再び繰り返すのであると思うだけであろう。もし空間関係を意識しているとすればそれは無限に延長した直線に於て一定の間隔を隔てて同一の事情Aが起こって行くというに過ぎないであろう。併しもし仮に同一のAなる点に帰ったということを何かの手段で知り得るならばこの生物は直線という概念に矛盾を発見する筈である。というのはロッツェによれば直線とは距離に外ならぬのであるから、この場合最大の距離が距離のないことを意味することとなる。生物はそれ故知覚に於てはともかく、論理的にはこの矛盾を避けることを強要される。従って空間の三次元性を予想することを強要される。即ちもし生物が空間表象を持つならばその持つと仮定された二次元は必然的に三次元に拡張されねばならぬと(Metaphysik, S. 249―252)。併し球面はリーマン空間の平面そのものではなくして既に述べたようにそのユークリッド空間に於ける表現に過ぎない。ロッツェは表現を空間そのものと見誤っているのであるからこの批難は批難そのものとしては当っていないと云わねばならぬ。併しロッツェの云い現わす処は直観空間が必然的に三次元でなければならぬということに外ならない。ロッツェに従えば英知的生物がこのようにして二次元から三次元に移るべく余儀なくされると同時に之を遂行し得るのであるが、同様にして吾々が三次元から四次元に移るということは云われない。何となれば二次元から三次元に移る必然性は一つの矛盾に由来したのであるが吾々は三次元に於てそのような矛盾は発見出来ない、且又吾々は四次元の直観を事実持つことが出来ないのであるから(同上 S. 252―257)。直観空間は三次元的でなければならぬであろう。カントの空間が直観であることを承認する限りたとえ空間が範疇へ結び付いた構想力によって成り立つと云ってもそれをば直観の規定であるこの三次元性を脱したものと考えてよい理由は何処にもない。空間は範疇へ結び付くにしても範疇そのものではない。範疇に従いながら(den kategorien gem ss)範疇Aへ空間固有な制限を加えているものと考えねばならぬ。カントが in Gedanken ziehen と云うも吾々は四次元に線を引くべく構想することは出来ないのである。勿論客観化された直観空間は三次元であるとしても之を成り立たせるかの構想力の順次総合そのものは三次元ではないと云われるかも知れないが、併しかく云うならば寧ろこの順次総合そのものは次元を持たぬものと考えるべきであろう。構想力の順次総合自身は次元を持たずに却って次元を産むものでなければならぬ。併し産まれるものは三次元の外はない。それ故この順次総合は三次元ではないにしても三次元を産むものでなければならぬ。又空間の直観そのものとしては次元は決定出来ないのであってある意味での反省によって始めて三次元となるのであると云うかも知れないが、反省されて三次元となるものは始めから三次元でなければならぬ。それではカントの空間はn次元の幾何学の基礎となることは出来ないのであるか。
ss)範疇Aへ空間固有な制限を加えているものと考えねばならぬ。カントが in Gedanken ziehen と云うも吾々は四次元に線を引くべく構想することは出来ないのである。勿論客観化された直観空間は三次元であるとしても之を成り立たせるかの構想力の順次総合そのものは三次元ではないと云われるかも知れないが、併しかく云うならば寧ろこの順次総合そのものは次元を持たぬものと考えるべきであろう。構想力の順次総合自身は次元を持たずに却って次元を産むものでなければならぬ。併し産まれるものは三次元の外はない。それ故この順次総合は三次元ではないにしても三次元を産むものでなければならぬ。又空間の直観そのものとしては次元は決定出来ないのであってある意味での反省によって始めて三次元となるのであると云うかも知れないが、反省されて三次元となるものは始めから三次元でなければならぬ。それではカントの空間はn次元の幾何学の基礎となることは出来ないのであるか。そこで私はカントが考えた幾何学と直観との関係を多少徹底させて見なければならぬ。「形像の生産に於ける生産的構想力のこの順次総合の上に延長の学(幾何学)はその公理と共に基き、その公理は感性直観の先験的制約を云い現わす」(K. d. r. V. S. 204)と云うようにカントに於ては幾何学の対象と直観空間とは直ちに一と考えられるのであるが、直観そのものと直観の公理とは何と云っても一応別なものと考えなければならぬ。公理から矛盾律によって始めて他の命題が帰結するにしても如何なる命題も総て直観内容でなければならぬ点に於てそれは公理と少しも異る処はない。ただカントによれば公理は「直接に確か」であるというのである。併し直観が直接に確かであるとか直接に確かではないとかいうことはそれは直観の判断であって直観そのものの立場ではない。直観そのものは総て直接でなければならぬ。最も煩瑣な証明を必要とする定理の内容も決してそれだけ間接であるのではない。「直接に確か」であると云う「直接さ」は直観それ自身の「直接さ」ではなくして直観の判断のそれである。直観そのものには前後はない。それはただ「論証」に於てのみあることである。公理はこのような論証の出発点に外ならない。それ故公理は直観から一定の内容を特に「直接」なるものとして引き出す処に始めてなり立つと云うの外はない。公理によって直観があるのではなく直観によって公理があるのである。それでは直観が直観の公理となることは何を意味するか。それは直観に思惟が結び付くことでなければならぬ。併し茲に云われる直観は生産的構想力と解釈された処の形式的直観なのであるから構想力が単なる所謂直観ではなくして範疇に結び付いたものでなければならぬ以上、それが思惟と特に「結び付く」と云うのは不当であると云われるかも知れない。併し明らかに構想力が範疇であるのではない。又構想力が範疇を内に全く包むのでもない。構想力(それは感性である)はあくまで範疇の外になければならぬ。そして而もそれは範疇に「従う」ものでなければならぬ。それ故構想力としての形式的直観は始めから概念に結び付いているものではなくして実は結び付き得る可能性を持っているということにすぎない。直観に思惟が改めて結び付くのでなければならぬ。そして思惟に真に結び付き得る処に空間の直観の特徴があるのである。経験的直観の結び付き得るものは経験的概念にすぎない。空間の直観に於てのみ純粋思惟がその demonstrativ な力を充分に発揮し得るのである。直観の公理とは思惟された直観であると云うことが出来る。空間の直観は自由なる思惟へ結び付くこと(公理)によって思惟そのものの力を借りて自らの内容を規定し得ると共に、自由なる思惟は空間の直観へ結び付くこと(公理)によって空間の直覚に基きつつ之を否定することなくして之を自由に超えることが出来る。n次元空間の公理はかくしてのみ始めて成り立つことである。何となれば思惟そのものにとっては三次元を四次元に拡張することは、たとえそれが感性的には不成立であるにしても、決して矛盾を含むものではないのであるから。空間を図式と考えればそれが三次元でなくてはならぬ処にその感性があり之を矛盾を含むことなくして越えて行く処で知的であるとも云えよう。そしてかかる可能性を持つ処に形式的直観の形式的直観たる所以がなければならぬ。もしそうでなければ空間は単なる経験的直観と選ぶ処はない筈である。以上のように解する時カントの立場は何の困難も含むものではない。今もし思惟が空間直観に対して持つこの自由を茲に認めないとすれば、即ち空間直観が始めから思惟と結び付いて了っているならば、独りn次元の空間概念が不可能であるばかりではなく、吾々は如何にして異った公理の上に立つ種々なる幾何学の空間を考え得るかが理解出来ない。そして之はカントが恐らく陥ったであろう処の困難である。カントは空間直観と思惟とを不当に密接に即ち不動な関係に結び付けたために、公理は直観の同語反覆的な裏面となり、一定不変なものとならなければならなかった。カントの考えからすれば私が先に述べたように直観空間が質的に平面性を持つならばそれはまた平行線公理を意味することとなり従って非ユークリッド幾何学と矛盾せねばならなくなるであろう。このような困難を脱する唯だ一つの道は公理を一定不動なものとすることを捨てること、即ち空間の直観に対する思惟の自由を認めることでなければならぬ。それはとりも直さず直観と直観の公理とをあくまで区別することに外ならない。即ち「直観空間」は幾何学の対象としての「幾何学的空間」とはその概念の内包に於ても外延に於てもあくまで区別されねばならぬこととなる。その区別の一斑を吾々は直観空間の三次元性に発見するのである。
今までのことを茲に反覆すれば、一つ、直観空間は規範性を持ち、二つ、直観空間は幾何学の対象とは別である、ということとなる。之だけのことを決めておいて私は物理的空間が如何にして成り立つかを考えよう。物理的空間という言葉は云う迄もなく一般に用いられているものであるが、その独立の存在は必ずしも承認されているものではないであろう。「幾何学的及び物理的空間の区別には何の根拠もない。ただそれは数学者にとっては空間は物理的な物体から抽象された空間的形像であるに対して、物理学者にとってはそれが物理的対象であり、空間的形像はただその形式に外ならない」。「この区別はただ吾々の主観即ち観察の視点にあるものに過ぎない、空間そのものはあくまで区分出来ない一者である」(L. Nelson, Kant und Nichteuklidische Geometrie, S. 26 ff.)と考えられはしないか。かくすれば物理的空間は要するに幾何学的空間に没し去るものとなるであろう。併し私はかかる疑問に対しては然りとも否とも答え得ると思う。二つの空間が何かの意味に於て同一でなければならぬということは考察の結果によるというよりも寧ろその出発点でなければならぬ。何となればもし両者の間に直接の結び付きがないならば吾々がそれを共に「空間」と呼ぶことさえ無意味となるのであるから。併し同時に空間が結局あるただ一つのものに結び付かねばならぬとしても吾々はその故に空間がただ一種でなければならぬと考える理由は少しもない。すでに私が幾何学的空間と直観空間との区別を指摘したように前者が後者に基きながらも結局後者とは区別されねばならなかったことから見ても空間をただ一種のものと見做すのは独断でなければ無造作の故である。吾々は本質的に種々なる空間が可能であることを許さなければならぬ。所謂「観察の視点」こそこの種々なる空間の存在を意味するに外ならない。併しもしネルソンの言葉から何か積極的なものを見出そうとならば、それは幾何学と物理学との間の固有に緊密な関係であろう。この固有性によって幾何学的空間と物理的空間とは区分することの出来ぬ一者であると臆測されるのでもあろう。併し種々なる空間の可能性を考える時この関係は物理的空間の独立を否定する結論に達する代りに却って物理的空間が如何にして独立するに至るかの理由を明らかにするに役立つ筈である。幾何学的空間と物理的空間との区別をこのようにして否定しようとする見方に対して之と同じ結論に達しながら或る意味では之と正反対の立場ともなるべきものを私はヘルムホルツの空間説に見出し得ると思う。ヘルムホルツに従えば幾何学に於ける測定は「合同の原理」に基きこれは又剛体の完全に自由な運動の可能性に基くものである(Ueber die Ursprung und die Bedeutung der geometrischen Axiome.)。そしてこの合同が図形の位置や方向や運動の道には無関係に行なわれるということは空間の測定を可能にする事実 Tatsache なのである(Ueber die Tatsache, welche der Geometrie zugrunde liegen.)。幾何学の公理が如何にして物理学へ応用されうるかという問題は、幾何学がかかる事実の上に建つものと考えられる時初めて理解され得る。同一の条件と同一の経過時間とに於て同一の物理現象が行なわれるような空間量を「物理的に等値」であると呼ぶならば、かかる等値な空間量は剛体の運動例えばコンパス及び定規によって規定される。この物理的等値という事実のみが空間量の完全に決定されたる客観的にして唯一なる性質なのである。それ故このような事実に基く幾何学は実際、物理的幾何学と呼ばれる筈である。物理学に応用される幾何学はこの物理的幾何学なのであるから、その応用の可能性は当然なものとして疑いを
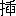 む余地を残さないものである(Die Tatsache in der Wahrnehmung, Beilagen.)。処が事実の内容 realer Inhalt を含みその公理が表象の単なる形式ではなくして実在の世界 reale Welt の諸関係によって決定されるこの物理的幾何学は、ヘルムホルツによればかのカントの考えたような空間の生具的な不動な直観形式とその公理とから成り立つ純粋幾何学とは明らかに区別されねばならぬ(同上)。かかる純粋幾何学が物理学に応用されるということは全く偶然なことに過ぎない、それは「空間の関係のみを云い現わすものでは全くなくただ剛体の運動の力学的関係のみを云い現わす処のかの物理的幾何学とは何の関係を持つものではない」という。さて物理的幾何学はヘルムホルツ自身の云うようにリーマンの「n次の多様」としての空間をその対象とするのであるから、その対象は一方幾何学的空間を意味せねばならぬ。併し又それと同時にそれが力学的関係のみを云い現わす以上それは物理的空間を意味せねばならぬ。茲に於て両者の区別はネルソンと同じく否定されることとなる。併し一方所謂カントの純粋幾何学の可能を許すとすればその対象としての幾何学的空間と以上の両者とは全く独立であると云わねばならぬ。この意味に於て幾何学的空間と物理的空間とは単に区別されるばかりではなくその間の関係が全く断たれるとさえ云わなければならなくなる。併しながら両者のこのような没交渉は数学と物理学との予定調和、数学が物理学に対する必然的応用を信ずる多くの科学者及び哲学者の同情を得ることは非常に困難であるであろう(A. Kneser, Mathematik und Physik 参照)。のみならず或る意味に於て両者の相即を主張し又或る意味に於て両者の完全な没交渉を帰結するヘルムホルツの幾何学及び空間に対する思想には経験論に共通な困難が潜んでいる。即ち如何にしてヘルムホルツのような思想からして幾何学に apodiktische Geltung を見出し得るかという疑問である。この困難を脱するものは云うまでもなくカントの空間説に外ならない。それ故物理的空間はカントの空間説に始めて正当にその成立の根を見出すであろう。
む余地を残さないものである(Die Tatsache in der Wahrnehmung, Beilagen.)。処が事実の内容 realer Inhalt を含みその公理が表象の単なる形式ではなくして実在の世界 reale Welt の諸関係によって決定されるこの物理的幾何学は、ヘルムホルツによればかのカントの考えたような空間の生具的な不動な直観形式とその公理とから成り立つ純粋幾何学とは明らかに区別されねばならぬ(同上)。かかる純粋幾何学が物理学に応用されるということは全く偶然なことに過ぎない、それは「空間の関係のみを云い現わすものでは全くなくただ剛体の運動の力学的関係のみを云い現わす処のかの物理的幾何学とは何の関係を持つものではない」という。さて物理的幾何学はヘルムホルツ自身の云うようにリーマンの「n次の多様」としての空間をその対象とするのであるから、その対象は一方幾何学的空間を意味せねばならぬ。併し又それと同時にそれが力学的関係のみを云い現わす以上それは物理的空間を意味せねばならぬ。茲に於て両者の区別はネルソンと同じく否定されることとなる。併し一方所謂カントの純粋幾何学の可能を許すとすればその対象としての幾何学的空間と以上の両者とは全く独立であると云わねばならぬ。この意味に於て幾何学的空間と物理的空間とは単に区別されるばかりではなくその間の関係が全く断たれるとさえ云わなければならなくなる。併しながら両者のこのような没交渉は数学と物理学との予定調和、数学が物理学に対する必然的応用を信ずる多くの科学者及び哲学者の同情を得ることは非常に困難であるであろう(A. Kneser, Mathematik und Physik 参照)。のみならず或る意味に於て両者の相即を主張し又或る意味に於て両者の完全な没交渉を帰結するヘルムホルツの幾何学及び空間に対する思想には経験論に共通な困難が潜んでいる。即ち如何にしてヘルムホルツのような思想からして幾何学に apodiktische Geltung を見出し得るかという疑問である。この困難を脱するものは云うまでもなくカントの空間説に外ならない。それ故物理的空間はカントの空間説に始めて正当にその成立の根を見出すであろう。第一批判の dritte Analogie には「凡ゆる実体は空間に於て同時に知覚される限り完全なる相互作用にある」と云われるが、この空間はカント自身特に何の説明も加えていない処から見ると之を私がこれまでカントに於て見出し来た直観空間と解釈するのが自然であるように見える。そうとすればこのような物理的な実体の相互作用の場となる意味に於て物理的な空間は特に直観空間と区別される手懸りがないかのようである。普通云われるようにカントの直観空間を絶対的空間と呼ぶならば今の場合これも物理的な絶対的空間と呼ばれてよいであろう。処が一方カントは凡ゆる絶対的運動の存在を否定し従って一切の物理的空間※[#下側の右ダブル引用符、U+201E、383-下-11]empirischer Raum“は相対的であることを主張する。相対的空間と相対的空間とを含むものは又相対的空間でなければならぬ。唯だあり得る一切の相対的空間を終局に於て包むと考えられた理念としてのみ絶対的空間が要請されるにすぎない(Metaphysische Anfangsgr
 nde der Naturwissenschaft. Phoronomie.)。今もし始めの第三批論の絶対空間と後の理念としての絶対空間とが同一であるならば茲には何の矛盾も起きない筈である。併しその場合には直観空間と考えられた始めの絶対空間が後の物理的な相対的空間にどう関係するかということが直ちに問題となる。吾々は直観空間が如何にして物理的空間となるかの問題に来る。もし又前の絶対空間と後の理念としての絶対空間とが直ちに同一とは考えられないとすれば、物理的空間は絶対的と考えられ又同時に凡ゆる物理的空間は相対的でなければならぬと主張することによって、それは一つの矛盾に陥るように見える。今この矛盾から脱れる道は絶対乃至相対に二つの異った意味を注意することの外にはない。即ち前の物理的空間は直観空間と考えられるという意味に於て絶対的であり後の物理的空間は運動系と考えられるという意味に於て相対的でなければならぬ。併しこの場合にも吾々は物理的空間と考え得るものが如何にして直観空間から運動系の空間となり得るかの問題に来る。それ故何れにしてもカントに於ては物理的空間は直観空間と関係させられることによって始めてその成立の根を与えられるのでなければならぬ。
nde der Naturwissenschaft. Phoronomie.)。今もし始めの第三批論の絶対空間と後の理念としての絶対空間とが同一であるならば茲には何の矛盾も起きない筈である。併しその場合には直観空間と考えられた始めの絶対空間が後の物理的な相対的空間にどう関係するかということが直ちに問題となる。吾々は直観空間が如何にして物理的空間となるかの問題に来る。もし又前の絶対空間と後の理念としての絶対空間とが直ちに同一とは考えられないとすれば、物理的空間は絶対的と考えられ又同時に凡ゆる物理的空間は相対的でなければならぬと主張することによって、それは一つの矛盾に陥るように見える。今この矛盾から脱れる道は絶対乃至相対に二つの異った意味を注意することの外にはない。即ち前の物理的空間は直観空間と考えられるという意味に於て絶対的であり後の物理的空間は運動系と考えられるという意味に於て相対的でなければならぬ。併しこの場合にも吾々は物理的空間と考え得るものが如何にして直観空間から運動系の空間となり得るかの問題に来る。それ故何れにしてもカントに於ては物理的空間は直観空間と関係させられることによって始めてその成立の根を与えられるのでなければならぬ。カントに於ては純粋直観は経験的直観の極限と考えられる。経験的直観に於ける感覚の一定量が次第に減じて零となる時純粋直観となる(K. d. r. V. S. 208)。直観空間はカントも考えたように一面に於てこのような虚空間 leerer Raum としての意味を失うことは出来ない。直観空間と感覚乃至知覚との関係は更に立ち入ってどう考えられるか。空間内に於ける形、量というような「純粋な規定」はアポステリオリに常に経験に於て与えられうるものをアプリオリに表象するが故に、吾々はそれを「現象の予料」と呼ぶことも不可能ではない(S. 209)。即ち直観空間は感覚を予料するものと考えられる。直観空間の内に這入って来る感覚はすでにそれに於て予料されてあるものでなければならぬ。感覚は直観の形式に対する直観の単なる内容というに過ぎない。それは全く直観空間そのものの下に原理上従属して了う立場にあるのであって直観空間に対して自らの特殊の立場を主張するものではない。かく考えて見ればこの場合の感覚は全く消極的であると云う外はないであろう。併しカントを離れて考えて見る時吾々は事実空間表象に於ける感覚の重さをより尊重する見方に逢着するのである。空間表象に於て感覚をより積極的に見るものは心理学に於て最もよく行なわれる空間知覚の概念でなければならぬ。カントのように空間を直観と見る代りに、空間を直観と知覚との和とも云うべき空間知覚と見るのであるから、知覚はそれだけ積極的となるわけである。もし心理学が一般にその方法論上の制約からして直ちに吾々の今の問題に結び付き難い困難を持つことを指摘し従って空間知覚に就いての議論を無用であると主張されるならば、吾々は意識をそれに固有な立場で観察する現象学を以て之に代えてもよいであろう。既に先に私はベッカーを引用して空間知覚の分析に触れたのである。併しベッカーも示すように空間知覚には種々なる段階を区別しなければならぬ。而もかかる段階は単なる区分ではなくして一つの順序を現わすものに外ならない。原始的なものから最も発展したものまでの階級を意味するものに外ならない。かの等質空間とはかかる階級の最高位に在るものであった。即ちそれは空間知覚の発展の終局と考えられねばならぬ。併し発展のこのような終局とは元来何を意味するか。のみならず他方ではこの等質的空間はそれ以前の段階の空間をその規定として内に含み得る性質を持つものと云わねばならぬ。orientierter Raum と雖も立ち帰って見れば等質的空間の内に於て orientieren されるのでなければならぬ。かく他の総ての空間知覚を内に含むとは元来何を意味するか。それは明らかに等質的空間が特殊の価値を有つことを示している。等質的空間はあらゆる他の空間知覚の発展の終局となり又その基となり得る価値を持つのである。勿論現象学の課題から云う時之以上出ることは出来ないかも知れない。併し認識の妥当性の modalit
 t から見る時等質的空間のこのような特殊の価値とは私が最初に決定したることによって実は実在の認識の規範であると云わなければならぬ。この規範の故に所謂等質的空間が何かの意味に於て終局的なものとして現われたに過ぎない。かく考えれば所謂空間知覚も規範としての空間の内に包まれて了うと云うの外はない。空間知覚そのものには規範性はない。視空間と触空間とそれだけでは唯一の空間に結び付くということは保証されないことである。之を唯一の空間に落ち合わせるようにするものは空間知覚の外に求められる空間の規範性と云わなければならぬ。すでに述べたようにカントの直観空間は正に之であった。それ故空間知覚と雖も原理的に規範としての直観空間そのものの下に従属する立場を離れるものではない。空間知覚に於いて認められるように見えた感覚の権能は依然まだ消極的であると考える外はないと思う。
t から見る時等質的空間のこのような特殊の価値とは私が最初に決定したることによって実は実在の認識の規範であると云わなければならぬ。この規範の故に所謂等質的空間が何かの意味に於て終局的なものとして現われたに過ぎない。かく考えれば所謂空間知覚も規範としての空間の内に包まれて了うと云うの外はない。空間知覚そのものには規範性はない。視空間と触空間とそれだけでは唯一の空間に結び付くということは保証されないことである。之を唯一の空間に落ち合わせるようにするものは空間知覚の外に求められる空間の規範性と云わなければならぬ。すでに述べたようにカントの直観空間は正に之であった。それ故空間知覚と雖も原理的に規範としての直観空間そのものの下に従属する立場を離れるものではない。空間知覚に於いて認められるように見えた感覚の権能は依然まだ消極的であると考える外はないと思う。感覚が真に積極的になり得ないのは客観界の唯一性とも云うべきこの規範性が常に感覚を超越した直観空間に求められているからである。規範性を何かの意味に於て感覚乃至知覚自身の内に見出すことが出来るならばそれによって始めて直観空間の立場を離れることも出来るであろう。併しこう云っても自らの内に見出されたものが直観空間の規範そのものであるならばそれは要するに直観空間の規範性であって積極的なる感覚乃至知覚のそれではない。それ故正しく云えば感覚が独立するためには自らの内に直観空間の規範そのものではなくして而もそれに相当する規範性を見出すことが必要となる。勿論このような独立な規範性を見出し得たにしてもそれによって感覚が直観空間から完全に独立して了うと云うのではない。あくまで直観空間の規範に支配されていながらなお且それ自身に独立な新しい領域を造り出すのである。それでは直観空間に相当する規範性とは何であるか。私はすでに直観空間と幾何学の対象との区別を指摘したのであるが、幾何学の判断乃至命題の apodiktische Geltung は幾何学が直観空間から由来する処に成立すると云わねばならぬ。即ち直観空間の実在認識の規範に由来するのでなければならぬ。直観空間は経験に規範として先立つという意味に於てアプリオリでありそれに従って幾何学は経験から独立に妥当するという意味に於てアプリオリなのである。勿論幾何学の先験的妥当性そのものが直にこの規範性であるのではない。それが規範性の意味を持ち得るのはただそれが実在の認識に応用される時に限るであろう。併し少くとも直観空間の規範に相当するあるものが幾何学であることだけは明らかである。それ故今もし直観空間の規範に相当する規範性を求めるならばそれは正に幾何学が応用される処に成り立つ筈である。直観空間と幾何学的空間との区別を明らかにした以上かくして求められた規範性が直観空間の規範そのものではないのは云うまでもない。幾何学が感覚乃至知覚に応用される時始めてこれに独立な規範性があり得るのである。感覚が真に積極的となるのである。感覚乃至知覚の間に幾何学的関係が成立する時始めてそれは直観空間から独立した意味を得てくるのである。併しこの場合もしカントの考えたように幾何学が直観空間の「純粋な規定」となるという意味に於て(図式としての図形などは之である)経験に対するその応用を云々するのであるならば、それは先に述べた所謂現象の予料の外ではなく、其処には感覚の積極的な権利は少しも見出すことが出来ない。カントは感覚の積極的な権利を認めることなくして幾何学の経験に対する応用を論じたために応用された結果は要するに直観空間の内容規定の外ではなく、其処から直観空間とは独立な何物かが生じるという可能性が全く断たれているのである。もしカントの考えた処のものを幾何学の直接の応用と呼ぶことが出来るならば、今の吾々の場合はその間接の応用と呼んでよいでもあろう。それでは幾何学の経験に対する間接の応用とも云うべきこと即ち感覚乃至知覚の間に幾何学的関係を成り立たせるとは何を指すか。それは即ち物理学の根本的規定とも云うべき測定の成立に外ならない。物理学にとっては測定し得るもののみが存在し得るのである。私は茲に測定と計量とを厳に区別したいと思う。後者が数と延長との直接な先験的な対応であるのに対して前者はこの対応関係が更に或る経験的な手続きによって現実に見出された結果を意味するのであるから相対性原理の教えるように空間の測定は必然的に時間の測定を含み時間の測定は光速度というような物理学的要素によって始めて成立するものである。また測定は測定者の存在即ち測定の原点を予想せずしては不可能であるが、而もこの原点は計量幾何学の原点とは直ちに同一ではない。測定の原点の間には相対的運動の可能性を許さねばならぬのであるから。併し測定は云うまでもなく計量を予想せずには不可能である。感覚乃至知覚の間に幾何学的関係を成り立たせるとはそれ故計量幾何学を之に応用するということに外ならない。幾何学が経験に応用されることの最も徹底したものは寧ろ今のこの場合でなければならぬと思う。かく応用されて生じる測定量の体系即ち測定の座標系はもはや単なる計量幾何学の対象でもなく、又直観空間の単なる内容規定でもないであろう。それは感覚を含んでいる。所謂「物理的空間」とはこれでなければならぬ。
物理的空間はもとより直観空間から由来するには相違ない。併しそれは第一に直観空間に於ては消極的と考えられる感覚の積極化を含むことによって直観空間とはその材料を異にしている。第二にそれは感覚の積極化を含む時幾何学の数量的規定を必然的に測定としてその内容にとり入れなければならなかった。而も直観空間にはこのような数量的規定は必ずしも本質的ではない。第三に幾何学の数量的規定は直観空間の三次元性を超えたものである以上物理的空間も亦三次元に限定される理由を必ずしも持たない。ミンコーフスキーの四次元の世界はその一例である。勿論人も云うようにミンコーフスキーの世界空間は直観空間の内容規定の内に尽きない点に於て仮構に過ぎぬと考えられるかも知れない。併し直観空間に対して仮構であるものが総ての意味に於て仮構であるのではない。寧ろこれは物理的空間としては正当な存在を持つものの一つであると私は思う。空間に感覚的内容が真に結び付くためには物の時間上の変化が更に一つの独立な次元となって付け加えられるということは寧ろ物理的空間の重大な特質と云わなければならぬ。吾々が普通常識的に空間と呼んでいるものは正しくこのような物理的空間の素朴なものであると思う。ミンコーフスキーの世界の如きはその最も精錬された成果であると云うべきである。物理的空間は空間の直観とあくまで区別されねばならぬ。次に又物理的空間は幾何学的空間とは明らかに同一ではない。幾何学的空間がたとえ射影幾何学の対象のように純粋に質的であるのでなくして座標による計量幾何学の対象と考えられる時でも、それは計量の座標系の体系であって、まだ決して測定の立脚点の体系ではない。物理的空間はあくまで幾何学的空間とも区別されねばならぬ。それ故に物理的空間は独立の意味を持つ一種の空間として成立することとなる。物理学に対して物理的空間が如何に重大な基礎となるかを考えて見る時このことは愈々著しくなるであろう。
(一九二四・一一・二〇)