〈一 和算とは〉
日本の数学を普通に和算という。和算とは洋算に対しての名称であり、主として維新後に呼びなされた。けれどもこの名称の行われたのは、数学がひとり西洋伝来のもののみにあらず、わが国にも前から厳として存在し、価値の高いものであったことを、この名称によって指示しているのである。西洋の数学が学校教科に採用されつつある頃に、かくのごとき現象の見られたのは決して無意義のことでない。和算というのは前にもいわれたことがある。その頃には漢算に対する和算であり、また和術もしくは倭術とも称した。天元術の器械的代数学に依頼するものは漢算であり、支那伝来の算法であるが、天元術の高次方程式を避けて簡便に算盤の解法に訴え得るものを賞用して、これを和術と呼んだのである。この点にいわゆる和算、すなわち日本の数学の理想が極めて明瞭に顕われている。単純化を貴ぶ精神が無くして、なんぞ、この種のことが起きて来ようぞ。算盤は支那で行われ、わが国へは支那から伝えたことに疑いはないが、しかし支那では日常の計算用に行われたのみに過ぎない算盤が、日本では複雑な数学の単純化のために重用せられ、そのために方程式の逐次近似解法や級数展開法の発達を促すことにもなった。その結果は極めて重大である。しかも支那ではそういう事情はついに見られなかった。これ故に特に和術、和算の名称が用いられ、漢算と区別しようと企てたのも、当然のことであろう。その区別を立てた和算家の間に、支那では見られなかった特殊の発達が顕現したのも、自然の勢いであったろう。
〈二 和算から洋算へ〉
事情すでにかくのごとくなるが故に、天文暦術においては支那西洋は優れているけれども、数学の一科に至ってはわが神州は世界に冠たりと考え、優秀な能力を自ら誇ったものであるが、少なくも支那に対しては、当然の誇りであった。西洋の天文暦術や理化学、航海砲術等が盛んに学習されたにもかかわらず、和算家が依然として多く西洋から学ぶことをしなかったのも、一方にはこの自負心あるがためであったろう。もちろん、三角法や対数などは西洋から伝えられたものを好んで研究し教授し、これを卑しむとか、これを避けようとしたのでもないから、ことさらに西洋の数学に接触しないように努めたわけでもないが、天文暦術家などに比して、その接触の機会に乏しかったという事情もあるが、常に独特の優秀観を有するが故に、悠然として独自の道を進むこともできたのであったろう。故に西洋数学の学習が大勢上から必要になってからもこれに対して和算と称して、一時は対抗の態度も現われないでは済むまい。しかし学科課程上の西洋数学の採用は世界の角逐場裏に出て、科学の力で世界と争わなければならぬという状態になったので、軍事や工芸など学ぶものの必要からどうしても、西洋の数学が必要であるから、そのための必須のことであって、ひとり和算家の力でその大勢の赴くところを阻止し得べくもないのであった。故に高久守静のごとき極端の和算主義者は極めて強く反抗したにかかわらず、和算の有力家中には自ら洋算を修めて、その教授の任に当たったものも少なからず、和算家は次第に凋落し、ついに明治二十年前後の頃に至って和算の勢力は地に堕ち、西洋数学の教授法は整い、新しく研究の業績もあげられることになるのである。故に維新後から明治二十年過ぎの頃までは、学校教科書の整頓と、教科書の作製と、西洋数学書の翻訳などが最も主要な事項となる。鏡光照のごとき和算時代に相当の独創能力を発揮した人物も独自の研究を止めて、数学講議録の発行等に全力を集中するようになった。川北朝鄰、岡本
一方には長沢、上野、中条、鏡、田中
これら明治維新後より同三十五年に至るまでのわが国の数学教育史については、理学博士小倉金之助氏著『数学教育史』に新研究が説かれているから、私は識者のこれを参照されんことを望み、併せて社会学者の側から適切な評論の出ることを期待する。同書には明治三十五年に数学教授要目が制定されたが、時の文部大臣菊池大麓及び大学教授藤沢利喜太郎編纂の教科書の内容に近いものであることを指摘し、かつ欧米諸国で数学教授の改革運動が始まっており、その要目の規定は世界の大勢に逆行したものであったとして筆をおく。小倉博士のこの書は、すこぶる数学教育界の注意をひき、教授上に少なからざる参考の料とならんとするの機運が見える。
〈三 和算の起こり〉
和算は支那の数学を基礎として発達した。そうして全く江戸時代のものであった。奈良朝時代の頃にも支那の制度によって数学が教授されたこともあるが、その実行の程度は今においてこれをつまびらかにすることができない。しかもさまで行われたものではなかったらしい。鎌倉、室町の武家時代には数学に関する事蹟の知られたものも少なく、かつさまで見るべきものはなかったらしい。暦法上において一の宣明暦を採用して七、八百年という長い年期間にわたって、ついにこれを改変しなかったことからでも、その事情は充分に察し得られる。武家時代の社会状態は、応仁乱後になると著しく変動する。旧勢力が倒れて新勢力がこれに代わり、軍事や経済生活上にも新しい活動を見る。美術も発達すれば、医学もまたその面目を一新する。この時に当たって数学もまた発達しなければなるまいと思われる。けれどもほとんどその史実に接することができない。ただ大導寺駿河守が北条氏の世子の教育に当たって、軍勢、兵粮、築城等の必要上から算用の習練から始めなければならぬと主張したということがあり、清水宗治は備中高松城で秀吉のために水攻めにせられ、切腹に際して、遺子への遺言状に算用を大切にしなければならぬことをいい、織田信長は天正七、八年頃から全国の検地に着手し、豊臣秀吉もまた遺志を継いだのであろうか、天正十三年頃から同じ事業に着手し、長束正家は算用に明るいがために秀吉に用いられたということであり、これらのことは支配者たる武家の間に数学の必要が起きつつあったことを語るものである。
故に豊臣秀吉が毛利重能を朝鮮または明に遣わして算法を学ばせたという伝説があるのも、その史料が明瞭でなく疑わしいけれども、しかも数学の必要に迫りつつあったことを示すところの伝説と見てよろしい。重能は京都の二条京極の辺に住し、天下一割算指南の看板を掛けて教授し門人も多かったという。その門下からでた吉田光由は洛西嵯峨の角倉家の一族にして、著わすところの『塵劫記』は極めて広く行われた。この書はわが国で色摺版画の用いられた最初のものということであり、また絵なども多く入れられ、興味深い書き方をしたものである。広く長く行われたのも畢竟そのためである。外国との交通貿易や河川の開通や嵯峨本の印刷等に関して功績の著しい角倉一族から光由がでたのは偶然ではあるまい。光由は肥後侯細川忠利に聘せられて算術を教授したことがあり、没後には略伝を加賀候へ書いて差し出したことがあって加賀候との関係も思われるのであり、諸大名の間に数学を学ぶ必要も多少は感ぜられて来たのであろう。
〈四 『改算記』と『算法闕疑抄』〉
『塵劫記』と前後した頃から数学教科用の書物は幾らも作られているが、『塵劫記』ほどに行われたものはない。後の『改算記』『算法闕疑抄』などは、これについで広く用いられたものである。『塵劫記』が出たのが寛永四年(一六二七)であり、爾後若干年間はこの種初期和算書の著作を主とする時代であった。この頃の諸算書を見るに、築城、河川、売買貸借、測量検地、度量衡、金銀の換算、租税、木材、その他の実用に関するもの多く、卑近な商工業用とともに武士階級に必要なるものも説かれている。これに加うるに趣味的のものに富むのが特色である。この時代には算数をもって諸侯に抱えられたものが幾人もあり、これらの人々は測量や土木事業や、経済関係のことなど担当することが多かった。浪人して算学を学び、これを教授しているものなどが必要に応じて召し抱えられたのであろうが、武士は算盤を手にすることを賤しみながらもその必要を思うたことは当然であろう。
和算は支那の数学から出発しながら、単に支那の数学を翻訳したというものではない。円周率なども大工などの間で用いられたらしいものが、一般に採用され、支那算書とは初めから色彩を異にした。そうして吉田光由が寛永十八年刊の『塵劫記』において十二の問題を提出してから諸算書にこれを解き、また新問題を提出して一種の競技が始まり、やや後れて数学の問題及び答術を絵馬に仕立てて諸社寺に奉納することも始まった。これは全く数学を芸術として取り扱ったのである。この数学の絵馬というものは、おそらく日本独特のことであったろう。芸術趣味の豊かな日本の国にふさわしいことであった。和算家の趣味は主として芸術として開拓したところに存する。和算家は常に芸に遊ぶということをいい、会田安明のごときは数学が云々の条件を具備しなければ「人に賞観されない」というようなことをもいっている。芸術として鑑賞するのが何よりの主眼であったのである。
私は先に『改算記』と『闕疑抄』という二部の算書の名をあげた。『改算記』とは先輩の諸算書に誤りが多いので、これを改訂した著述であることを意味し、『闕疑抄』もまた同様に疑わしいものが多いから、その疑いを闡明するという趣意である。この二つの書名から見ても、初期の和算書は如何に誤りの多いものであったかを、極めて雄弁に物語る。和算家は趣味性に富み、また難問題の研究に努力を惜しまなかった。けれども、誤りを犯したものは実におびただしい。初期の諸算書においてしかるのみならず、後代になっても引き続いて同様であった。和算家は粗漏勝ちであったという大きな弱点を暴露しているのである。
『算法闕疑抄』は礒村吉徳が万治三年(一六六〇)に著わすところ、巻末に一百の新問題を提出したが、この諸問の中には極めて注意すべきものがある。関孝和が『闕疑抄答術』を作り、その業績中の主要なものの大半はこれに基づいたのではないかと思われる。関孝和の業績が和算の創始ともいうべき価値あるものなるにおいて、『闕疑抄』の問題はその歴史的重要性が思われよう。新問題の提出がどれだけの役目をしたかは、ほとんど計り知るべからざるほどに大きい。この礒村吉徳はもと浪人であって、二本松藩に抱えられ安達太郎山から二本松城に引いた水利はこの人の施設にかかり、今も現に存在して、私もその現状を見たのである。礒村吉徳の閲歴といいその著書といい、『塵劫記』以来、関孝和以前における代表的のものといってよかろう。
〈五 『古今算法記』〉
関孝和の業績が現われる前には、一方には沢口一之の『古今算法記』(寛文十年、一六七〇)が出たことも注意すべき一つの要点である。初期和算書の多くは算術的のものであるが、元の朱世傑の『算学啓蒙』(一二九九)が豊公の時代に伝えられ、後にこの本によってかどうかはしばらくおき、日本で翻刻も作られ、また所載の算法たる天元術も了解され応用され得ることになる。沢口のこの書中では『算法根源記』の一百五十の問題をこの天元術によって解くまでに進んだ。そうして方程式に両根のあることをも注意しながら、唯一の解答を得ることを理想とし、問題を翻狂すなわち病的だと解して、与えられたる数を改めたものである。その処理は感服し難いけれども、支那では唯一根のみしか注意していなかったのに比すれば、明らかに進歩であり、かつ後の進歩を促成しなければ止まぬものであった。関孝和の方程式論ともいうべきものの開拓はこれから発足したのではないかと思われる。なお巻末に十五の新題を提出したが、普通の天元術では解き難きものであり、関孝和は演段術を用いて解いたのである。天元術は算木すなわち小さな木片を使って代数演算を行うところの器械的算法であるが、演段術は天元術から出ながら、算木を用いずして筆算式に行うところの新数学であった。日本の筆算式新代数学はかくして創始された。この新しい創意があるために、後の発達を促進することも著しいのであり、巧みに代数演算の運用されたのは、近代の西洋を除いては、ひとりわが日本の和算あるのみに過ぎないのも、この創意に基づくのである。漢字を記号に使いながら、支那ではついに発現しないものであった。具体的の意義ある漢字を用うるが故に、西洋で記号使用の代数学が発達するのよりも、割合に容易に発展し得たようにも思われる。けれどもこれに関する関孝和の功績はまことに大きい。〈六 関孝和の業績〉
関孝和の業績と称せられるものの中にも、剰一術及び招差法などいうものは明らかに支那にも前に存したのであるが、しかし一般にその算法の原則をも巧みに了解して適切に運用したことが思われる。支那の方程、すなわち一次連立方程式解法を極めて巧妙に応用して諸般の研究をよくしたと思われることのごときはその手腕の凡ならざるものであった。要するに関孝和はある原則をもとめて深く研究を進めたために、大きな業績を建て得たのである。関孝和はその伝記にも、その業績にも従来世に伝えられたものは、疑わしいことが多く、この人最高の発明といわれた『乾坤之巻』所載の円理のごときは、その実は門人建部賢弘から始まったらしいのであるが、またその業績として確実なものの中でも〈七 建部賢弘の帰納法〉
建部賢弘は関孝和が天才的の能力を発揮する人であったことをいっている。これに反し、建部自らは天才的でないから、着実にこつこつと一から二へ、二から三へという風に、帰納的に探会するという研究方法を賞用したことを主張する。その著『不休綴術』(享保七年、一七二二)はこの主張を実現するために作られたのであり、いわば一種の数学方法論の述作である。こういう研究方法は関孝和ももちろんこれを用い、これによって重要な業績をもあげているけれども、建部が探会という二字でいい表わしたところの方法を中心に取って、まとまった方法論に作り上げたのは、建部賢弘の著述を措いては他に見られぬのである。この頃からして、そういう研究方法は一般に数学界を風靡したともいうべく、続々と帰納的の探会に拠った算法が現出した。この算法、この方法論は一方には建部賢弘その人の人物を表現すると同時に、またその当時並びに以後における和算界の傾向を示すものである。そうして関孝和と建部賢弘との人物並びに学業の相違はあたかもよく建部がこれを喝破し得たように思われる。関孝和は如何にも天才的であった。故に天元術の器械的代数学を学んでは、これを運用しやすき筆算式のものに改造する。一次連立方程式の解法に通じては、これを行列式の構成並びに展開に役立たせ、普通人の容易に企て及ばぬ多くの発明創意をも能くし得たのである。この偉大なる関孝和にして、前にいったごとき重大な過誤を犯したというのも、つまり天才的に想い及んだのであり、充分に吟味することをしなかったための結果に過ぎないと思われる。もし実地に当たって検証することをしたならば、容易に補訂し得たのであったろう。和算界に誤りの極めて多いことは、和算の終末まで続くのであり、刊行された多くの算書に先輩の発表中の誤りを訂したもののはなはだ多いことからでも思われる。上州の萩原禎助のごときは、和算終末の大家であるが、諸算書の問題を綿密に研究してこれを補訂するのが、この人の最も主要な事業であった。内田五観が『古今算鑑』中に発表した、梯形内に楕円と四円を容れた問題のごときも、計算上に符号を錯誤して誤ったのだとかいうことである。平野喜房の『浅致算法』付録に相接する三円間に
〈八 秘伝の公開〉
かくのごとき欠陥がありながら、しかも幾多の業績があげられ、全体としてまことに立派なものであったのは、要するに天才の閃きであり、また着々と歩武を進めて研究を遂行する熱情に富んだがためである。会田安明が諸種の問題を捉えていろいろとこれを検討し、種々の場合を尽くして遺漏のないことを期したごときは、この後者の好個の標本的の一例となる。会田は千数百巻の著述があり、この人ほど著述に富んだものはない。会田は山形の人、江戸に出て関流の数学を学ばんとしたが、覇気に富める彼は、関流の学閥に屈することができないで、藤田定資に対抗して一大論争を惹起するに至った。時あたかも、天明寛政中のことにして、国民の自覚の高まりつつあった時代であり、この論争が人気に投合して、会田の名望が極めて高められたのも、世態の傾向に無関係ではない。これより先、久留米侯有馬頼
 は関流山路主住に師事したが、関流秘伝の算法を取りまとめて『拾
は関流山路主住に師事したが、関流秘伝の算法を取りまとめて『拾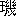 算法』を作り、これを公刊した。想うにこれは山路が伝授料をぼったりなどするために憤慨して、大名という地位を利用して、秘伝を公開したのであったろう。会田安明はその後を受けて論争を開始したのであるが、ある意味では有馬頼
算法』を作り、これを公刊した。想うにこれは山路が伝授料をぼったりなどするために憤慨して、大名という地位を利用して、秘伝を公開したのであったろう。会田安明はその後を受けて論争を開始したのであるが、ある意味では有馬頼 の後継者とも見られよう。会田は才気の優れた人物であるが、秘伝を主とする当時においては、関流の門に入らなければ秘伝を受ける便宜がない。故に藤田の門を叩きもした。藤田は関流の大立物という地位を擁してともかく尊大に構えている。二人の人物の相違は、時代の精神と相俟って互いに争わなければならぬことになったのである。
の後継者とも見られよう。会田は才気の優れた人物であるが、秘伝を主とする当時においては、関流の門に入らなければ秘伝を受ける便宜がない。故に藤田の門を叩きもした。藤田は関流の大立物という地位を擁してともかく尊大に構えている。二人の人物の相違は、時代の精神と相俟って互いに争わなければならぬことになったのである。和算界に秘伝ということがあったのは、古くからのことであった。関孝和のごときも秘伝は容易に伝えなかったということである。秘伝は和算には限らず、すべての学芸にわたってそうであったが、和算もまたその風習に従ったのである。これは封建社会の当然の事情であったろう。最高の秘伝は特殊の高弟にのみ授けられ、次から次へと伝わってここに系図を構成する。家の系図と同じように、算家系図というものも、幾らも作られている。かくして数学にも流派を生じた。その諸流派の中で最も盛大なのが関流であった。会田安明が流外にあって、この関流の最大権威と対抗せんとしたのは、剛胆なる彼にして初めてよくなし得るところであった。そうしてその対抗により充分に効果をもあげ得たのである。この対抗が続けば続くだけ、会田は益々自信を強めたらしく、いかにしてか関流の秘伝算書も多くその手に入り、発明創意もまた次第に多きを加うるに至った。会田安明は才気あるものが旧套の権威に対抗して、光輝ある成功をかち得た適例である。この論争の事情から見ても、権威を擁する藤田定資は極めて卑劣であり、陰険であったらしい。会田安明は論争中において、自ら一つの流派を創め、これを最上流と称した。
初め関孝和は高弟荒木村英に皆伝したが、他の高弟建部賢弘には皆伝しなかったといわれている。けれども、この伝えはおそらく確実なものではあるまい。京都の算家中根元圭は建部について、その高弟となり、久留島義太の天才を認めて幾多の便宜を与え、久留島が多く創意があったのも、その結果に負うところであろう。久留島の友人に松永
〈九 和算の教授〉
かくして文政天保の頃に至打、有力な算家が多く輩出し、和田寧のごとき大家も出た。和田寧は学力造詣がはなはだ優れていたにかかわらず、酒ばかり飲んで生計にも追われ、算学の外に手習いの師匠をもしたほどであり、発明術を売って酒に替えたともいわれている。この故に当時の諸大家はこの人について伝授を受けたものも多く、またこれを基礎として研究を進め、従って和田寧の円理は比較的容易に諸方に広められた。その功績は偉大であるが、一般世間からはほとんど知られないのであり、天保十一年(一八四〇)に没した時のごときも、諸算家すらも顧みないほどの気の毒な有り様であった。これに反して内田五観、長谷川この時代には和田や内田、長谷川等は江戸にいるが、しかし諸地方でも諸大家が多く輩出して上州の斎藤父子、熊本の牛島盛庸等のごときは、すこぶる見るべきものがあった。これには諸藩で藩校を置き、数学の教授も行われることになったことに関係があるが、また今いう斎藤父子でも江戸の長谷川でも武士階級の人ではないのであり、民間から有力な算家が出ることにもなったのである。長谷川寛は全く数学教授を稼業にしたものであり、教授のためには非常の努力を積んだのである。故にこの人の手で『算法新書』が作られて、数学教科書の極めて良好なものが成立し、養子
これと同時に地方では遊歴算家なるものが盛んに活躍した。山口
かくて和算は天文暦術や砲術航海等のことに関して西洋の学問が伝えられつつある間において、これらの関係も多大にありながら、比較的に西洋の影響を受けることが著しからずして、その終末に至った。和算家は洋算の勢力に対抗せんことを欲し、和算の勢力を維持したい希望もあったけれども、もはや時勢の必要には如何ともすることができないで、和算は次第に地歩を失うこととなった。けれども京浜鉄道の開設に際して小野友五郎がその測量に従事したり、地租改正の時に備中の和算家平松誠一が諸県下に出張して測量術など教授したごとき事実も多く遺されたのであり、和算から洋算に代わる過渡期には和算家が世用を充たしたことも少なくないのである。
和算家はこの過渡期において実用の方面に活動したというだけではなく、和算の起きた初期からして実用のことに深い関係の〔を〕もったのは、もとよりいうまでもない。試みに和算書のあるものを採って点検するがよい。ある特殊のものを除くの外は、必ず多くの実用上の問題を取り扱っていないものはない。和算家として測量等のことに関心を持たなかった人もいないようであるし、和算を教授する以上は別して初心の人へは日常生活に関係ある問題を課したものであった。もしこの種の事項を抽出して、これから立論するときは、和算は実用的の関係、経済生活上の関係のみから動かされて発展したものでもあるように論ずることも決して不可能ではあるまい。しかしながらかくのごときは一面観に過ぎないであろう。
〈十 和算と芸術〉
しからば他に如何なる方面があるか。芸術的に取り扱ったことが、極めて重要な地歩を示す。『塵劫記』が優良な教科書であったというのも、趣味深くできているからである。『塵劫記』には継子立の問題というものが出ているが、これは実子と継子が十五人ずつあり、輪形に環列せしめて、ある一人から数え始め十人目に当たる毎にふるい落として最後に残った一人を相続人にしようというのであるが、継子十四人まで数え抜かれたときに、一人残された継子が抗議を提出し、これからは逆の順に数えることにされたいと申し出たので継母もこれに同意し、そうして遂にその継子一人が最後に残って父の家を嗣ぐことになったというのである。この問題は如何に見ても、日常生活、経済もしくは社会関係のものではない。すべて趣味の問題に外ならない。しかもこの種のものは、わが日本人の芸術的生活に極めて好く適合したのであり、和算の初期からして単に実生活の関係にのみ局限せずして、数学を芸術的趣味的に取り扱って行こうという精神が極めて濃厚であったことを示す。後になっても和算には、非実用的のものが多いのであるが、すべてこれは芸術の精神をもって開拓したので、ここにはなはだ偉大な発達をも遂げ得たのである。この芸術的趣味的ということは、一方に実用的精神のはなはだ大切であるのに対して、決して、これに劣らざる大切な要素であって、和算家の間にその精神が極めて濃厚であったことは、名状し得べからざるほどに崇高な強味であった。もしこの精神に欠くるところがあったならば、和算は決してあれだけの発達を成就し得なかったに違いないのである。
この精神は、もちろん和算の学修によって初めて開発されたのではない。わが国文化の諸方面にわたって一般に顕現しているのであり、おそらくわが国民性の長所ともいうべきものであろう。わが国中世の戦闘史上において武士道の精華を発揮したもののごときも、全く芸術的に処したものなることを見る。仇討に苦心を積んだのも芸術の大きなものであった。和算の開発上にもその同じ精神が、著しく趣味的に現われて、良好な成果を結ばないでは済まないのであった。ここにおいて私は和算史の全般をもって、一大芸術の展開であったと見ないではいられないのである。和算が実用を離れて、芸術的趣味的に発達したのは、武士という比較的に閑散な階級が存在し、この閑散な武士階級を中心として開拓されたことにもよるけれども、さらに、一層根本的に芸術的精神の旺盛なものが働いたのではないかと思われる。しかしながら和算は主として武士階級を中心に消費経済の都会であった江戸の産物であるのに対し、実験的科学らしいものが、西方から起きて来たという著しい事実があるのは、その点からは経済的生活の反映があったと認めなければならぬのも、またもちろんである。
〈十一 和算と社会〉
関孝和が江戸から出て和算を創始した時代に当たり、貞享の改暦をよくした渋川春海は、近畿の人であった。寛政の改暦は大阪の暦学者高橋至時及び間重富が徴せられて、これをよくし得たのである。初め豊後の人麻田剛立は脱藩して大阪に来り、医を業として生計を立てつつ、暦術星学の研究に専念した。至時、重富等が剛立の門に入って益々その研究を進めた。これがためにわが国の暦学は一大革新を遂げたが、幕府は江戸の天文方がよくなすなきをもって、これを召し出してそのことに当たらしめたのである。この時伊能忠敬が高橋について学ぶに至り、高橋は星学研究の必要上から伊能の測地事業を推挙し、そうしてラランデ暦書の訳解の事業も天文方の手で遂行されることとなり、それから暦局内に翻訳局が設けられ、一方に高橋景保、渋川景佑等の手で『新考暦書』等が作られ、一方には訳官の人達によって『厚生新編』のごとき大部の書の翻訳書が作られ、ここにおいて蘭学の発達は極めて著しいものとなった。この事業は天文暦術の関係が、最も主要な基底を成して進んだのであり、それから他方面のことが付随したものであったことが、決して見逃してはならないところであろうと思う。この翻訳事業において天文暦術書中に西洋数学に接触したことの多かったのはいうまでもないのであるが、しかも数学の関係においては、さまで重大な影響をしたらしくもないようである。これは天文方の暦学者と当時の専門算家との間に密接な関係が乏しかったからでもあろうが、また双方ともに密接に関係を結ぶことを心がけたらしい形跡もないのである。この一事から見ても当時の数学が如何に実用方面から没交渉であったかが充分に思い及ばれるであろう。
数学がかく天文暦術とすらも、密接な交渉を付けなかったごとき事実は、決してほめたものではないが、しかしそういう状態にあっても、ずいぶん目醒ましい発達が成就し得られるということは、注意すべきことと思われる。
ここにおいて思うに、数学の教育上にはなるべく、実生活と関係を密にすることが望ましいであろう。けれどもまたこれを趣味的芸術的に取り扱って、若き心の数学に対する趣味を開発し、進境を打開すべき曙光が全く認められないではあるまい。私は和算の発達に顧み、趣味的芸術的生活は生活上の重大な要素であろうことを考えたい。